Particles vs. strings
Predictability
The main problem in high energy theoretical physics today is predictions, especially for quantum gravity and confinement. An important part of predictability is calculability. There are various levels of calculations possible:- Existence: proofs of theorems, answers to yes/no questions
- Qualitative: "hand-waving" results, answers to multiple choice questions
- Order of magnitude: dimensional analysis arguments, 10? (but beware hidden numbers, like powers of 4π)
- Constants: generally low-energy results, like ground-state energies
- Functions: complete results, like scattering probabilities in terms of energy and angle
It is easy to write down the most general theory consistent with special (and for gravity, general) relativity, quantum mechanics, and field theory, but it is too general: The spectrum of particles must be specified, and more coupling constants and varieties of interaction become available as energy increases. The solutions to this problem go by various names -- "unification", "renormalizability", "finiteness", "universality", etc. -- but they are all just different ways to realize the same goal of predictability. Unfortunately, most solutions to these problems simply sweep them under the rug, solving one form of the problem and replacing it with another: For example, "renormalization", a systematic way of eliminating infinities in certain calculations, eliminates ambiguities at one stage only to have them reappear later. Other approaches look only at "low" energies, and thus effectively ignore most of the problem altogether. (But "low" might be ridiculously high by current standards for very weak forces, such as electromagnetism or gravity.)
Score card
| topic | particles | strings |
|---|---|---|
| dimension | Predictive particle theories do not exist in dimension D>4, and thus effectively predict the correct result D=4 (3 space, 1 time). | Known string theories do exist in D>4. They effectively predict "critical" D=10, 11, or 26. If the observable dimensions are constrained to 4, predictive power is lost. However, useful particle models can be accomodated. |
| supersymmetry | The standard calculational method for particles uses an approximation method ("perturbation") that involves adding correction terms. When the infinite number of terms is summed to find an exact answer, predictive power is lost in the absence of supersymmetry. Thus, particle theory predicts supersymmetry. | Known string theories have serious difficulties already at low orders of perturbation in the absence of supersymmetry, so string theory predicts supersymmetry. |
| graviton | Maximal supersymmetry requires (super)gravity, so the existence of the graviton (particle of gravitational force) is predicted by that particle theory. However, treating the graviton as a fundamental particle leads to a loss of predictability, even at low orders of perturbation. A possible alternative is to treat the graviton as a composite state of other particles: Such theories have been constructed, but have not yet been shown to be predictive. | The existence of the graviton is required by known string theories, and thus predicted: This is true for the superstring, which has maximal supersymmetry (although it may be hidden in some formulations). It is also true for the bosonic string; however, that string has some consistency problems. Known string theories retain their predictive power in their critical dimension at all orders of perturbation; however, summation leads to the kind of effects (hidden dimensions) that are expected to destroy predictability. |
| black holes | A black hole is defined by an "event horizon", which is the border of the part of space where even light must hit the singularity, which is in turn defined as the region where the theory breaks down. Thus the very existence of black holes in a theory of gravity indicates its inadequacy. (However, black hole singularities might be avoided by formulations in "Euclidean space", with imaginary time.) Black hole solutions are not expected in a composite-state theory of gravity. | Some advantages are found in the description of black holes, but the situation is unclear. |
| unification | Predictabilty strongly restricts the class of allowed models, but there is still a lot of freedom. Observed matter (quarks and leptons) can be unified, resulting in a unification of forces (less gravity, plus yet unseen forces), but requiring many yet unseen and un-unified "Higgs scalars" to break the symmetry. Supersymmetry introduces unseen particles as least as numerous as the known ones, and thus is not truly unifying. | String theories are essentially unique in their critical dimension, and unify all forces and particles, including gravity. But "compactification" to D=4 is far from unique, and destroys any advantages of unification. |
| confinement | Qualitative arguments predict confinement of quarks and gluons inside hadrons, but calculations are limited to low-energy properties of hadrons (or high-energy properties of quarks and gluons), and cannot calculate properties of any but the lightest hadrons. | Strings can describe properties of hadrons of all mass, and agree with qualitative properties of hadron scattering. But known string theories don't fit well to experiment, since they include massless hadrons. |
Final tally
- Particle theory correctly predicts D=4, string theory doesn't.
- Both particle and string theory have difficulty with unification.
- Both theories predict supersymmetry. Unfortunately, it hasn't been observed yet.
- Both strings and maximally supersymmetric particles predict gravity, but neither solves the problem of predictable quantum gravity in D=4.
- The experimental facts that hadrons behave like strings, and they are bound states of quarks and gluons, which can't be confined in D>4, indicates there are D=4 string theories we're missing. Such strings would not contain gravity, since hadrons have no corresponding (massless) "strong graviton". They would be based on the particle theory of quarks and gluons. Perhaps some generalization would include both hadrons and gravitons.
Possible solution:
A composite graviton might be necessary to solve the gravity problem in particle theory. A string that is a composite of particles (as for hadrons) might be necessary to solve the D=4 problem, which may be the root of all string theory's problems. Thus particle theory and string theory would be unified, and this unification would be a requirement to solve the problems of both theories. In fact, at least one of the known strings can be expressed as a composite of particles, but this particle theory has serious problems, probably related to those of the string theory.Is string theory a waste of time?
Considering that string theory has close to a monopoly on high energy theoretical physics nowadays, yet in over 40 years has failed to reach its promised goal, panic can easily set in about the future of this area of research. In response to the above question, I can think of at least 4 answers:- Don't blame the product for the advertisement. String theory has been grossly over-sold. It isn't even a "theory" yet, just a "model". It hasn't solved anything, much less everything. But just because it isn't everything doesn't mean it isn't anything. It has many interesting features, some of which have been reproduced in particle theory and proven useful, some of which haven't but would be desirable in a more realistic theory.
- That's what they told Columbus. (Besides "Stop killing Indians!") Similar arguments have been leveled against the space program, but exploration often has many rewards, such as serendipity. (And theoretical research is cheaper than spacecraft.)
- What's "string theory"? "String theory" is a very ambiguous term, just as "QCD" was in the 70's. Almost all of high-energy theory today is string theory, by definition. "String theory" can mean "supersymmetry", "general relativity", "differential geometry", "extra dimensions", "conformal field theory" (in either 2 or 4 dimensions), and a number of other things. Many papers on "string theory" make no use of string theory, but just use the words because their topic is related and they want to attract attention (good or bad). Many results used in papers, claimed to be features of only string theory, are in fact much more general.
- Compared to what? At this point in time, there are no more-promising solutions to many of the problems of high-energy physics. Of course, alternatives exist, and you are welcome to try some (I do), but most of the complaints leveled against string theory can be applied to them even more strongly. (In particular, watch out for theories that claim to solve some problem simply because it is too difficult to even see if they have that problem.)
- The masses of the observed strongly interacting particles (hadrons) with the same properties except for mass & spin, when plotted on a graph of spin vs. mass2, lie on parallel straight lines ("Regge trajectories").
- These same lines, when continued to negative mass2, describe high-energy scattering of hadrons @ small angles. Strictly speaking, this is already a property of Regge theory more generally. But string theories are the special case of Regge theories where this behavior can be described by a perturbation expansion, whose not-too-strong coupling implies the linearity of the Regge trajectories as well as the distinctively string property:
- At lowest order in perturbation (coupling constant), the scattering amplitude can be found by summing either the contributions where particles annihilate into a single particle which then splits back into 2, or the contributions where the 2 scattering particles exchange a single particle. Either sum gives the same, total result; summing over both would be double counting. This "duality" can be pictured by viewing the scattering as the merging of particles into the "worldsheet".
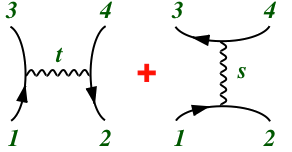 |
vs. |  |
Loop quantum gravity
As an example of the "Compared to what?" point, consider one alternative often mentioned, "loop quantum gravity". One way to describe this theory is as a lattice approach to gravity, replacing the spacetime continuum with a discrete set of points. But we already know a lot from lattice approaches to nonperturbative field theory, e.g., lattice quantum chromodynamics:- Problems with perturbation theory are not solved by nonperturbative approaches. The problems of "renormalizability" that appear in perturbation theory (especially for quantum gravity) return with a vengeance in nonperturbative approaches. (This has also been seen in more rigorous nonperturbative approaches to field theory, such as "constructive quantum field theory".) The lattice itself acts as a "regularization" of infinities, but the true problem of infinities is not eliminating them, but the ambiguities in eliminating them, which result in a loss of predictability. In lattice approaches, "non-universality" appears as ambiguities in the lattice description of the theory that do not disappear as one takes the limit of distances large with respect to the lattice spacing.
- Lattice calculations are prohibitively difficult. So difficult that even with modern day computer power it is all one can do to calculate with a lattice that is 32 units long on a side. Thus one cannot directly even address questions such as long-distance limits. (So far, lattice approaches have been used only to calculate constants, such as masses and couplings.)
- Fermions are difficult to describe. There are difficulties describing fermions, the basic constituents of matter, on lattices, already at the classical level. At the quantum level, there are further difficulties that make computations impractical. In particular, there is no known way on a lattice to describe "supersymmetry", a feature needed to solve renormalizability problems.
