Physics 105 Problem Set 10
Due: Tuesday, December 18, 2007, by 4:30 pm in 208 Jadwin.

Due to the second midterm, we will have just one long problem set due on Dec. 18. We strongly suggest that you start on this unit soon. At least do some Knight reading and some Learning Guide problems.

Required reading for this week and next:

-- Knight Chapters 16-19 (Most should be a review)
-- Fermi Sections 1-14 (don't worry about the partial derivatives at the end of section 14.)

Optional

-- It is a very good idea to warm up by doing problems in 103 Learning Guides 11 and 12 after you've done the required reading. LG 11 problems I, II, III, VI, and VII, and all the LG 12 problems are the important ones.

Problems to turn in:

Problem 10.1 Fermi, pg 10, number 1

Problem 10.2 Fermi, pg 10, number 4

Problem 10.3 Fermi, pg 45, number 3

Problem 10.4 A vertical cylinder 2.5 m tall is filled with 0.08 moles of an ideal gas at STP. Next, a piston of mass 1.5 kg is added to one end of the cylinder compressing the gas somewhat. It seals the cylinder but is free to move vertically. (1)What is the equilibrium height of the piston assuming that the gas is isothermal. (2)The piston is now displaced slightly and released. What is the frequency of oscillation?

Problem 10.5 Knight 19-72

Problem 10.6 Entropy is a state variable.

a) The left-hand p-V diagram shows two ways to bring an ideal gas from point a to point c: directly along the isotherm ac, or constant volume to point b, then constant pressure to point c. By directly calculating Delta S for the two paths, show that the change in entropy is the same for both.
b) Optional: not for credit, but try it if you like. You could do the same for the right-hand diagram, where the isotherm is replaced by an adiabat (and this changes the relations among the various p's and V's). Instead, use the fact that S is a state variable to derive the form of the adiabat, that is, the relation between p and V. Note: we aren't pretending to discover this -- it helps in your manipulations to know what you are after.

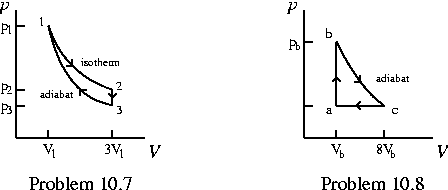
Problem 10.7 An ideal diatomic gas is taken through the cycle shown in the figure below. Determine for all three processes, in terms of p1, V1, T1, and R,

a) p2, p3, T3
b) W, Q, Delta U, and Delta S, all per mole.

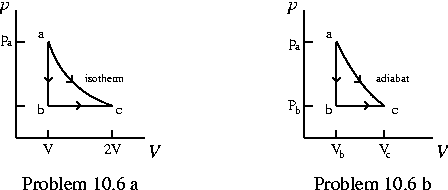
Problem 10.8 One mole of a monatomic ideal gas is taken through the reversible cycle shown in the (not-to-scale) figure below. Process bc is an adiabatic expansion, with pb=10.0 atm and Vb=1.00×10 -3 m3. Find:

a) the heat added to the gas,
b) the heat leaving the gas,
c) the net work done by the gas, and
d) the efficiency of the cycle.
e) What would the maximum possible efficiency be for any engine operating between the same maximum and minimum temperatures as this one?