Physics 103H Problem Set 3
Due: Friday, October 5, 2007

Students who are interested in enrolling in Physics 105 should solve and hand in these problems. They will be graded and will count towards your 105 grade. This is in addition to the normal 103 assignments. This set is to be turned in at the first Physics 105 lecture, Friday Oct 5, or by 4:30 PM in Jadwin 208. Reading: Phy103 assignment plus K&K 4.1-4.7.

Problem 1. Sports/power/work/food.

a) A strong human cyclist, weighing about 110 kg (including bicycle), can bicycle up a 3.1 percent grade at about 30 km/h. What is her or his power output in watts? in horsepower?
b) How does this compare to a typical human office worker climbing stairs in an office building at a rate of one floor every 20 s?
c) How many kilocalories (which are known as "calories" in nutritional information) would you have to eat every day to sustain each of these (relatively high) levels of activity for 3 hours per day?
d) A person with an active lifestyle eats 3 to 5 thousand kilocalories per day. Do you think that the production of mechanical work is the primary use of food calories?

Note: to do this problem, you will have to look up some conversion factors, and you will have to estimate the typical height per floor of an office building.

Problem 2. A particle of mass m experiences a force that depends only on the particle's position. The force is given by

Fx=6xy;   Fy=3x2-3y2;   Fz=0

Calculate the work done by this force as the particle moves from the origin (0,0,0) to the point (x1,y1,0) via these two paths:

a) (0,0,0) to (x1,0,0) to (x1,y1,0).
b) (0,0,0) to (0,y1,0) to (x1,y1,0).

Problem 3. En route to Tycho Magnetic Anomaly 1. A space station consists of a hub connected to a ring by four spokes. The whole station turns as a unit with period T to provide ``artificial gravity'' to the occupants, who, of course, walk around on the OUTER wall of the ring. Note: there is no real gravity in this problem. The spokes contain elevators to bring people and equipment to and from the docking port at the center of the hub.

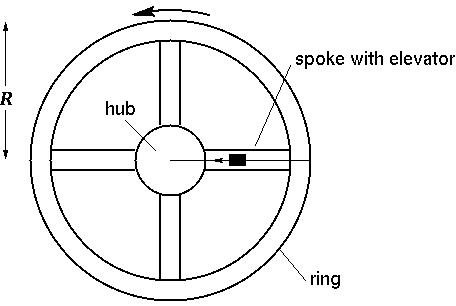2001 Space Station Assuming no friction and a massless elevator cable, how much work does the elevator motor do in bringing a load of mass M (including the elevator car), slowly and at constant speed, from the ring at radius R to the center of the hub? Without regard to your detailed calculations, is this work positive, or negative? Assume that the walls of the spoke keep the elevator car turning around the hub with period T and with negligible effect on the rotation of the station as a whole.

Warning: There is a strong temptation to use W=delta K here. In this case, however, the walls of the shaft are doing the work that changes the speed of the car, not the elevator motor.

Problem 4.

a) The potential energy of an object is given by U(x)=8x2-x4, where U is in Joules and x is in meters. (a)Determine the force acting on this object. (b)At what positions is this object in equilibrium? (c)Which of these equilibrium positions are unstable?

U(x)

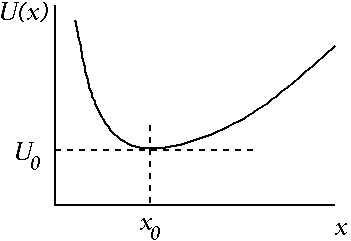
b) The figure shows a potential energy function U(x) for motion in one dimension that is arbitrary except for the fact that it has a stable equilibrium point at x0. Show that for small displacements from equilibrium, this system obeys Hooke's Law, that is, it acts just like a mass on a spring. What is the value of the "effective spring constant" k?

Hint: a Taylor series will tell you the behavior of U(x) near x=x0.

Note how general this is: for small displacements from equilibrium, (almost) everything acts like a simple spring! Given your derivation, can you think of an exception?


Problem 5.

K&K 2.34. However, please do not explicitly use the conservation of angular momentum.