Physics 105 Problem Set 5
Due: Thursday, October 18, 2007, by 4:30 pm in 208 Jadwin.

Reading
K&K 6.1-6.7

It is a very good idea to do the 103 Learning Guides 5 and 6. The problems that you turn in do not cover all of the material for which you are responsible!

Problems to turn in

Problem 5.1

A solid cylinder of mass m, radius R, and thickness (width) l is released from rest and rolls without slipping down a plane inclined at an angle theta to the horizontal.
(a) Draw a free body diagram and compute forces and torques to determine the angular acceleration and linear acceleration down the plane.
(b) Compute the kinetic energy of a rolling-without-slipping cylinder as a function of linear speed and compare with the gravitational potential energy to determine the linear acceleration down the plane. If you answer does not agree with part (a), explain.
(c) Now consider a 4-wheeled cart of total mass M with four wheels, each with radius r and moment of inertia I. Ignore friction in the axles or bearings. What is the acceleration a? What is the implication for a race on Hot Wheels track? (If you don't know what Hot Wheels are, ask one of your instructors!) What is the limit as I becomes small? To what is I being compared when it is said to be small?

Problem 5.2

A spool rests on a rough horizontal table. A massless thread would on the spool is pulled with force T at an angle theta to the horizontal.
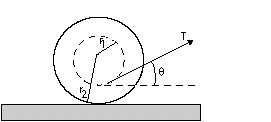(a) If theta=0, will the spool move to the left or to the right?
(b) Show that there is a critical angle, theta_0, for which the spool remains at rest. Assume that T is small enough so that the spool does not slip.
(c) At this critical angle, theta_0, find the maximum tension for equilibrium to be maintained. Assume a coefficient of static friction of mu_s.

Problem 5.3

K&K 6.8.

Problem 5.4

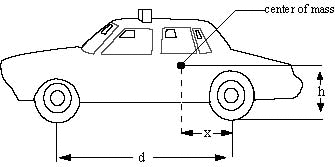
The center of mass of a car of mass M is a distance h above the surface of the road and a distance d-x behind the front wheels. The front and rear wheels are a distance d apart (d>x).
(a) If the car is at rest, find the normal forces exerted by the road on the two front and the two rear wheels, N_f and N_r respectively.
(b) What is the fastest the car can accelerate (that is, the maximum acceleration) before the front wheels leave the road? (Hint: consider dL/dt.)
Note: neglect the angular momentum of the rotating tires. Assume that the suspension keeps the axles fixed to the frame of the car. You may assume that the car has 4- wheel drive, though you will find that it doesn't matter.

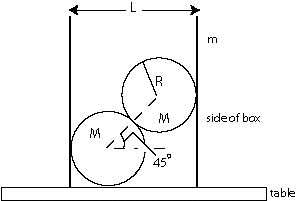
Problem 5.5

Two steel balls, each of radius R and mass M, are packed into a bottomless cylindrical thin-walled tube of diameter L =[2+sqrt(2)]R. The tube and balls sit on a table. There is no friction anywhere in the problem. Find the minimum mass of the tube m that will keep the system in equilibrium.