Reading for this week K&K Chapter 9

• Background information (some of which you have read already.)
  • K&K pp. 27-35
  • K&K pp. 80-86, 101-103 (these properties of gravity are very important, and we will probably not go over them in lecture.)
  • K&K Examples 4.5, 4.12, and section 4.9
• K&K 9 (skim examples 9.3)
• Optional.
  • Knight Ch. 12
  • As always, it is a good idea to warm up by doing problems in 103 Learning Guide.

Problems to turn in:

Problem 7.1 Warm-ups.

a) Show that the momentum of each particle in the center-of-mass frame of a two-body system is p^*=+-µv, where µ is the reduced mass and v is the relative velocity.

Parts b) and c) refer to circular orbits. Do them using simple considerations of uniform circular motion, not the heavy artillery of K&K 9!

b) For a circular orbit of small mass m about large mass M, find the relation between the kinetic and potential energy for this gravitational interaction.

c) Prove Kepler's third law for the case of circular orbits and the gravitational force: T² = kR³, where T and R are the period and radius of an orbit, again for M>>m. Find k for the Solar System.

Problem 7.2 K&K 9.5
Some hints:

-- Note that from the force law given, you can see that the relaxed length of this spring is zero.

-- In part b), the radial impulse is given in addition to the circular motion of part a).

-- In part b), make a useful energy diagram, i.e., one that actually illustrates the solution to part c).

Problem 7.3 Learning Guide 7, problem IV.

Problem 7.4 K&K 9.8

Problem 7.5 K&K 9.9

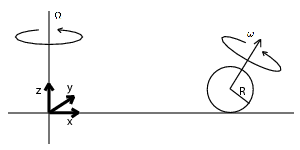
Problem 7.6
As shown below, a uniform ball of radius R rolls without slipping on a turn table that spins at angular frequency Ω along the positive z direction. Demonstrate that the ball follows a circular orbit (not necessarily centered on the axis of rotation of the turn table) given by dv/dt= Ω′ x v where v is measured in the lab frame. How does this equation produce a circular orbit? What is Ω′ ?

Note that although this problem is about orbits, the only role of gravity is to keep the ball on the turn table so that it can roll without slipping. You may want to start by finding an expression for the velocity of the ball in the lab frame. If you give a complete solution (ball positions, linear velocity, and angular velocity direction) for one of the possible orbits you will earn 5 points of extra credit.