References

1

L. Onsager,Crystal statistics I. A two dimensional model with an order-disorder transition, Phys. Rev. 65, 177 (1944)

2

C.N. Yang, The spontaneous magnetization of the two-dimensional Ising model, Phys. Rev, 85, 808 (1952)

3

B.M, McCoy and T.T. Wu, Theory of Toeplitz determinants and the spin correlation functions of the two-dimensional Ising model IV, Phys. Rev. 162, 436 (1967)

4

S.Ghoshal and A.B. Zamolodchikov, Boundary S matrix and boundary state in two-dimensional integrable quantum field theory, Int. J. Mod. Phys. A9,3841 (1994).

5

B.M. McCoy and T.T. Wu, Theory of Toeplitz determinants and the spin correlation functions of the two-dimensional Ising model V, Phys. Rev. 174, 546 (1968).

6

M.E. Fisher, Walks, Walls, Wetting and Melting, J. Stat. Phys. 34, 763 (1984)

7

B.M. McCoy and T.T. Wu, Theory of a two-dimensional Ising model with random impurities, Phys. Rev. 176, 631, (1968)

8

H. Furstenberg, Trans. Am. Math. Soc. 108, 377 (1963).

9

B.M. McCoy, Theory of a two-dimensional Ising model with random impurities III. Boundary effects, Phys. Rev. 188, 1014 (1969)

10

B.M. McCoy, Incompleteness of the critical exponent description for ferromagnetic systems containing random impurities, Phys. Rev. Lett. 23, 383 (1969)

11

R.B. Griffiths, Nonanalytic behavior above the critical point in a random Ising ferromagnet, Phys. Rev. Letts, 23, 17 (1969).

12

R. Shankar and G. Murthy, Nearest-neighbor frustrated random bond model in d=2: Some exact results, Phys. Rev. B36, 536 (1987).

13

D. Fisher, Critical behavior of random transverse field Ising spin chains, Phys. Rev. B51, 6411 (1995)

14

T.T. Wu, B.M. McCoy, C.A. Tracy and E. Barouch, The spin-spin correlation function of the 2-dimensional Ising model: exact results in the scaling region, Phys. Rev. B13, 316 (1976).

15

P. Painlevé, Acta Math. 25 1 (1902).

16

B.M. McCoy, J.H.H. Perk and T.T. Wu, Ising field theory: quadratic difference equations for the n-point Green's functions on the lattice, Phys. Rev. Letts. 46, 757 (1981)

17

M. Sato, T. Miwa and M. Jimbo, Holonomic quantum fields, Publ. RIMS Kyoto Univ. 14, 223 (1978); 15, 201 (1979); 15, 577 (1979); 15, 577 (1979); 15, 871 (1979); and 16, 531 (1980).

18

M. Jimbo, T. Miwa, Y. Mori and M. Sato, Density matrix of an impenetrable Bose gas and the fifth Painlevé transcendent, Physica D1, 80 (1980).

19

C.A. Tracy and H. Widom, Level-spacing distributions and the Airy kernel, Comm. Math. Phys. 159, 151 (1994); Fredholm determinants, differential equations and matrix models, Commun. Math. Phys. 163, 33 (1994).

20

K. Iwasaki, H. Kimura, S. Shimomura and M. Yoshida, From Gauss to Painlev' e: a modern theory of special functions, (Vieweg 1991, Braunschweig).

21

B.M. McCoy and T.T. Wu, Two-dimensional Ising field theory in a magnetic field: breakup of the cut in the two point function, Phys. Rev. D18, 1259 (1978).

22

A.B. Zamolodchikov, Integrable field theory from conformal field theory, Advanced Studies in Pure Mathematics, 19 ,641 (1989)

23

G.H. Wannier, The statistical problems in cooperative phenomena, Rev. Mod. Phys. 17, 50 (1945)

24

C.N. Yang, S matrix for the one-dimensional N-body problem with repulsive or attractive 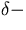$\delta-$function interaction, Phys. Rev. 168, 1970 (1968).

25

R.J. Baxter, Eight vertex model in lattice statistics, Phys. Rev. Lett. 26, 832 (1971).

26

A.A. Belavin, A.M. Polyakov and A.B. Zamolodchikov, Infinite conformal symmetry of critical fluctuations in two dimensions, J. Stat. Phys. 34, 763 (1984)

27

H. Au-Yang, B.M. McCoy, J.H.H. Perk, S. Tang and Y.M. Lin, Commuting transfer matrices in the chiral Potts models: Solution to the star triangle equations with genus >1, Phys. Letts. A123, 219 (1987).

28

S.Howes, L.P. Kadanoff, and M. den Nijs, Quantum model for commensurate-incommensurate transitions, Nucl. Phys. B215[FS7] 169 (1983).

29

R. Baxter, H. Au-Yang and J.H.H. Perk, New solutions of the star-triangle relations for the chiral Potts model, Phys. Lett. A, 128, 138 (1988)

30

R.J. Baxter, Chiral Potts model; Eigenvalues of the transfer matrix, Phys. Letts. A146, 110 (1990)

31

B.M. McCoy and S.S. Roan, Excitation spectrum and phase structure of the chiral Potts model, Phys. Letts. A150, 347 (1990)

32

G. Albertini, B.M. McCoy and J.H.H. Perk, Excitation spectrum and order parameter for the integrable N-state chiral Potts model, Nucl. Phys. B314, 714 (1989)

33

L. Onsager, discussion, Nuovo Cimento 6, Suppl., 261 (1949).

34

R.J. Baxter,Corner transfer matrices of the chiral Potts model, J. Stat. Phys. 63, 433 (1991).

35

R.J. Baxter, Functional relations for the order parameter of the chiral Potts model, J. Stat. Phys. 91, 499 (1998)

36

F.D.M. Haldane, ``Fractional statistics'' in arbitrary dimensions: a generalization of the Pauli principle, Phys. Rev. Letts. 67 (1991) 937.

37

B.L. Feigen and D.B. Fuchs, Verma modules over the Virasoro algbras, Funct. Anal. Appl. 17, 241 (1983).

38

R. Kedem, T.R. Klassen, B.M.McCoy and E. Melzer, Fermionic quasi-particle representations for characters of 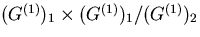$(G^{(1)})_1\times (G^{(1)})_1/(G^{(1)})_2$, Phys. Letts. B304, 263 (1993); Fermionic representations for conformal field theory characters, Phys. Letts. B307, 68 (1993).

39

A. Berkovich, B.M. McCoy and A. Schilling, Rogers-Schur-Ramanujan type identities for the M(p,p') minimal models of conformal field theory, Comm..Math. Phys. 191, 325 (1998).

40

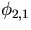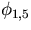A. Berkovich, B.M. McCoy and P.A. Pearce, The perturbations $\phi_{2,1}$ and $\phi_{1,5}$ of minimal models M(p,p') and the trinomial analogue of Bailey's lemma, Nucl. Phys. B519[FS],597 (1998).

41

B. Nickel, J. Phys. A (in press)

42

A. Guttmann and I.G. Enting, Solvability of some statistical mechanical systems, Phys. Rev. Letts. 76, 344 (1996).

43

B.M. McCoy and W. P. Orrick, Analyticity and integrability in the chiral Potts model, J. Stat. Phys. 83, 839 (1996)

44

R.J. Baxter, Exactly solved models, in Fundamental problems in statistical mechanics V, Proceedings of the 1980 Enschede summer school Ed. E.G.D Cohen, (North Holland 1980),109.