Rogers-Ramanujan Identities

1.

R. Kedem, B.M. McCoy and E. Melzer, The sums of Rogers, Schur and Ramanujan and the Bose-Fermi correspondence in 1+1 dimensional quantum field theory, in Recent Progress in Statistical Mechanics and Quantum Field Theory, ed. P. Bouwknegt et at. World Scientific (Singapore 1995) 195, hepth 9304056.

2.

A. Berkovich, B.M. McCoy and W. Orrick, Polynomial Identities, Indices,and Duality for the N=1 Superconformal Model Sm(2,4v), J. Stat. Phys. 83 (1996) 795 (hepth 9507072).

3.

A. Berkovich and B.M. McCoy, Generalizations of the Andrews-Bressoud identities for the N=1 superconformal model SM(2,4v), J. of Math. and Computer Modeling, 26 (1997) 37 (hepth 9508110)i.

4.

A. Berkovich, B.M. McCoy and A. Shilling, N=2 supersymmetry and Bailey Pairs, Physica A 228 (1996) 33.( hepth 9512182).

5.

A. Berkovich, B.M. McCoy and A. Schilling, Rogers-Schur-Ramanujan type identities for the M(p,p') minimal models of conformal field theory, Comm. Math. Phys. 191 (1998) 325. q-alg 9607020.

6.

A. Berkovich, B.M. McCoy, A. Schilling and O. Warnaar, Bailey flows and Bose-Fermi identities for the conformal coset models 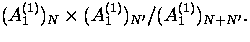$(A_1^{(1)})_N\times (A_1^{(1)})_{N'}/(A_1^{(1)})_{N+N'}.$Nucl. Phys. B 499 (1997) 621 (hepth 9702026).

7.

B.M. McCoy, Quasi-particles and generalized Rogers-Ramanujan identities, Proceedings of ICMP97 (in Press).

8.

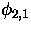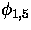A. Berkovich, B.M. McCoy, and P.A. Pearce, The perturbation $\phi_{2,1}$ and $\phi_{1,5}$ of the minimal models M(p,p') and the trinomial analogue of Bailey's lemma, Nucl. Phys. B519[FS] (1998) 597 hepth 9712220.

9.

A. Berkovich and B.M. McCoy, Rogers-Ramanujan identities: A century of progress from mathematics to physics, Proceedings of ICM98 Documenta Mathematica, Extra volume ICM 1998, vol. 3 (1998) 163.