Improved methods for hypergraphs

(talk at Adventures in Superspace, 4/19/13)

Dharmesh Jain and Warren Siegel

[arXiv:1302.3277]

Earlier work:

“Hypersymmetry”: N=2 supersymmetry — Fayet (’76)
⋮ (cf. “Bambi Meets Godzilla”)
Hypergraphs:

• Ivanov, Galperin, Ogievetsky, Sokatchev (’85)
• Gonzalez-Rey, Roček, Wiles, Lindström, von Unge (’97-8)
• Jain, Siegel (’09-12)

Background hyperfields: Buchbinder², Ivanov, Kuzenko, Ovrut, McArthur, Petrov (’97-’02)

This paper does for N=2 supergraphs what was done for N=1 by ...

Improved methods for supergraphs

Marcus T. Grisaru, W. Siegel (Brandeis U.), M. Roček (Cambridge U.). Jun 1979. 32 pp.
Published in Nucl.Phys. B159 (1979) 429

Cited by 742 records (INSPIRE)

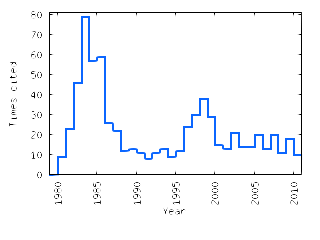⇐     Actual experimental data related to supersymmetry           ⇓

Cited by 910 (Google scholar)

Background field formalism

		N = 1		N = 2 (6D N=1)
quantum superfield		scalar		scalar
superspace		x, full θ		x, analytic (½) θ, (internal) y
representation		chiral		analytic
background superfield		spinor		spinor
superspace		x, full θ		x, full θ, no y
representation		real		real
nonrenormalization		obvious*		obvious*
effective action		x, θ		x, θ (no internal)

*As for N=1,
Quantum superfield is scalar prepotential of dimension 0;
background superfield is spinor (or maybe vector) potential with dimension > 0.

N=4 Yang-Mills

1-loop cancelations in N=4 Yang-Mills as formulated in N=1 or N=2 superspace:

		N = 1		N = 2
scalar multiplets		3		1
Faddeev-Popov ghosts		-2		-2
Nielsen-Kallosh ghosts		-1		1
total		0		0
vector multiplets		1		1
“extra” ghosts		0		1-2
total		1		0*

*Same propagator, different vertex ⇒ cancels only y-divergence δ(0).
In both cases, vector multiplets etc. contribute only @ 4-point & higher,
scalar multiplets etc. also @ lower-point.

Equations

In case there’s too much time left, some actual equations:

scalar/FP/NK propagator:		1 y₁₃² ∇₁ϑ⁴∇₂ϑ⁴δ⁸(θ₁₂) 1 ½k²
vector/XR propagator:		δ(y₁₂) y₁ ∇₁ϑ⁴δ⁸(θ₁₂) 1 ½k²
scalar/FP/NK vertex:		∫d⁴θ dy (◻̂-◻₀)
vector vertex:		∫d⁴θ dy y(◻̂-◻₀)
XR vertex:		∫d⁴θ d²y [-1 + y₁δ(y₁₂)](◻̂-◻₀)

Above are for just 1 loop (free quantum in background).
For vertices, use ∇_ϑ⁴ from propagator to make ∫d⁴θ ∇_ϑ⁴ = ∫d⁸θ.

Conclusions

1. Same kind of simplifications for N=2 as for N=1 (1 loop & higher)
2. Quantum field V (x, θ, y), where A_ϑ = 0;
   background fields A_θ, A_ϑ, where A_y = 0, trivial dependence on y
3. Classical action in analytic superspace d⁴x d⁴θ dy, nonlocal in y;
   effective action in “full” superspace d⁴x d⁴θ d⁴ϑ, no y
4. N=3 supergraphs (for N=4 Yang-Mills): in progress
5. Supergravity
6. 1st-quantization?

That’s a good question!

Quantum vertices (background appears only through ∇_ϑ⁴):

scalar:		-∫d⁴θ Ῡ(eV-1)Υ
vector:		∫d⁴θ d⁴ϑ dⁿy (-1)ⁿ n (eV₁-1)∙∙∙(eVn-1) y₁₂y₂₃∙∙∙yn₁
FP:		-∫d⁴θ (yb+b̄)LV/2 ⎡ ⎣ coth(LV/2) ⎛ ⎝ c- c̄ y ⎞ ⎠ + ⎛ ⎝ c+ c̄ y ⎞ ⎠ ⎤ ⎦

Nonlocality in y gets no background covariantization, since A_y = 0.