For prospective graduate students

Every March we get visits from undergraduate seniors (& Master's students) considering coming to Stony Brook for graduate school, asking for a description of my research. (See "Ph.D. applicants" for procedural details.) Most of my web pages are either too introductory, too advanced, or too narrow for that purpose. Some students have had quantum field theory or general relativity, or even string theory, some not, & even if they have they might not have covered them in the way I use them. (It is expected that classical mechanics, classical electrodynamics, special relativity, and nonrelativistic quantum mechanics are already well understood before tackling these topics.) This page is to give them an idea of what I do.

You might know from graduate-level courses...

Some of these topics are covered in a little more detail in my other web pages. (See in particular "Preparation for research" for details on what I consider these topics to be.) They are covered in great (but not infinite) detail in my book Fields. They are needed for research with me, but are taught in courses that are standard @ Stony Brook. If you are already well versed in them you may be able to start research early.

Feynman diagrams

Feynman graphs are a useful way to represent quantum field theory in terms of (relativistic) quantum mechanics. By representing antiparticles as particles going backward in time, these diagrams treat space & time on equal footing. S(cattering) matrices can be represented analogously to electric circuits, with junctions describing interaction points, & lines representing the worldlines of particles propagating freely between interactions. Each diagram gives a mathematical formula allowing its contribution to the S-matrix to be calculated.

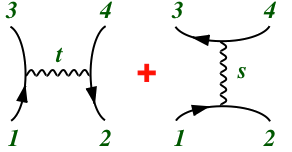
When the graphs have no loops ("trees") they are essentially classical field theory, except for the use of complex Green functions ("Stückelberg/Feynman propagators"). The expansion in the number of loops is a type of JWKB expansion, but expands in the power of coupling constants, rather than the long-distance/low-energy approximation of quantum mechanical JWKB. This perturbative expansion is the most useful approach to calculating S-matrices; nonperturbative alternatives generally are limited to low-energy results, such as relating coupling constants.

Yang-Mills & gravity

Yang-Mills theory is a self-interacting generalization of electromagnetism, where the particles mediating the forces themselves have charges. It is best described in terms of a "covariant derivative", －i∇ = p + A, where p = －i∂ is the total energy/momentum, A is the Yang-Mills field, or (minus) the potential energy/momentum, and by the correspondence principle －i∇ represents the "kinetic" energy/momentum, whose square gives －m². In electromagnetism there is a single 4-vector A, but in Yang-Mills there are more: E.g., for "gauge group" SU(2), which has 3 generators, there are 3 A's.

Since a massless vector (spin 1) has only 2 (circular) polarizations, 2 components of the 4-vector must not represent particles. In electromagnetism this is not a problem, but in Yang-Mills, 2 fermionic "ghosts" are used to cancel the 2 unphysical "longitudinal" polarizations in quantum calculations.

Gravity (general relativity) is a further generalization, where coordinate transformations are the gauge group. Since coordinates are already a vector, this means gravitons have spin 2. This theory is also best described with covariant derivatives which, as in electromagnetism & Yang-Mills, can act on fermionic/spinorial fields as well as bosonic. (Particles can be treated as fields by considering a continuum of "dust".)

Supersymmetry

Supersymmetry is a symmetry that relates fermions to bosons. Since these particles have not only different statistics but also different spins, its generator is itself fermionic & spin ½. This leads to it being tied to spacetime translations.

Just as the usual spacetime coordinates are associated with translations, fermionic coordinates can be assigned to supersymmetry. The resulting "superspace" is useful especially for quantum calculations. In particular, it treats all members of a supersymmetry "multiplet" simultaneously.

This symmetry thus has a spin-3/2 gauge field, the "gravitino" which, by supersymmetry, is partnered to the graviton: This is "supergravity". Due to its enlarged symmetry, the quantum properties of gravity (particularly the short-range/"ultraviolet" ones) are enhanced & simplified.

String theory

String theory generalizes point particles to strings, either open (with 2 ends) or closed. Its vibrational modes correspond to an infinite variety of particles of various spins & masses. The corresponding generalization of the worldline is a worldsheet. The "stretchiness" of the worldsheet means its Feynman diagrams contain many particle diagrams.

Attempts are being made to use it to describe strong interactions and/or quantum gravity:

String theory has features in common with the observed spectra & small-angle, high-energy scattering of hadrons. The Anti-de-Sitter/Conformal-Field-Theory correspondence is an attempt to relate this behavior to the framework of Quantum ChromoDynamics, which describes the observed large-angle, high-energy scattering of hadrons.
It also has better ultraviolet behavior for quantum gravity than even supergravity, and the enlarged symmetry allows unification of gravity with the Standard Model.

You may have glimpsed in undergrad/Master's research...

The following are some of the topics of my research. (See "What I'm working on now" for a bit more technical detail. See also "Research in theoretical high energy physics" for a broader but less deep classification of what other people here do in "hep-th".)

Extended supergraphs

Multiple spinors can be introduced to describe multiple supersymmetries, with a maximum of 4 for super Yang-Mills, & 8 for supergravity. Because of the enlarged symmetry enforcing more restrictions, S-matrices become simpler as the number of supersymmetries is increased. These simplifications are manifest in the appropriate superspace, allowing some properties to be obvious without calculation, & allowing S-matrices to be calculated more directly.

Part of my research is deriving & refining this extended superspace formalism, & performing the resulting S-matrix calculations. The classical part involves finding the "coset" superspaces, & where the superfields live on them. The quantum part uses a "background field" formalism, where the initial/final fields are treated differently from the "virtual" fields, the former being more covariant & composite, while the latter are simpler algebraically & more fundamental. (A simple analogy is electromagnetism, where the former is the Maxwell fields, while the latter is the gauge potential.)

Chiral string theory

By an unusual change in boundary conditions on the worldsheet, superstrings can be made to describe only a finite number of fields, all massless, but in arbitrary dimensions. Since string diagrams contain many particle diagrams, this provides a simpler way to calculate S-matrices for such theories.

My present research involves strengthening the relationship of this theory to conventional string theory, & extending known results to the quantum level.

F-theory

Supergravity theories have more symmetry than might be expected from just looking @ their spectra. These are symmetries of the action, but they do not preserve the vacuum: They are "spontaneously broken".

Some of this symmetry is more evident if one recognizes that the 10D supergravity of the massless sector of superstring theory can be derived from 11D supergravity, which is expected to be the massless sector of some "M-theory" that contains strings in the spectra of membranes.

Some other of this symmetry is manifested by doubling the number D of spacetime dimensions: The extra dimensions correspond to the number of times a string winds in various compactified periodic dimensions (up to all of them). There is then a "T-duality" between these winding modes & quantized (due to periodicity) momenta, resulting in an O(D,D) symmetry. (This is closely related to the chiral strings discussed above.)

All the symmetry should appear in an "F-theory" that includes all these hidden higher dimensions. It has a symmetry based on the "exceptional" (Lie) groups.

		F E_D+1/H_D
	⇙		⇘
M GL(D+1)/O(D,1)				T O(D,D)/O(D－1,1)²
	⇘		⇙
		S GL(D)/O(D－1,1)

I'm now working on completing the formulation of this theory on the worldvolume, deriving the form of the massless sector of the theory with the maximum symmetry, and using it to calculate S-matrices.