Taking the Particle out of Particle Physics

by Sylvester James Gates, Jr. and Warren Siegel

(originally appeared in Quotient, University of Maryland, April/May 1986)

Particle physics is the most fundamental area of science in that its goal is to reduce the wonderful diversity and complexity of our universe to a few simple mathematical laws. Until recently, the point particle was considered to be the ultimate building block of matter. The fundamental particles include quarks, gluons, electrons, photons, gravitons, and many others. One class of composite particles is the hadrons, which consist of quarks bound together by gluons. These include protons and neutrons, and the mesons which bind them together to form atomic nuclei. At the next level of complexity, atoms are formed from nuclei and electrons held together by photons. Finally, gravitons bind macroscopic bodies. All of these interactions have been incorporated successfully into the framework of quantum mechanics, with the exception of gravity, which is harder to investigate experimentally in this context, since it's too weak to observe at the microscopic level, the dominion of quantum mechanics.

Within the last two years there has been an explosion of interest in the possibility that geometric quantities other than points play a fundamental role in our description of nature. The next most complicated geometrical object is a (finite) curve, or string. The simplest string is the relativistic string, whose mass and tension are described by a single parameter, reflecting the fact that the vibrations of the string propagate at the speed of light. String theory may be the first successful synthesis of quantum mechanics and general relativity. Remarkably, there are indications that this synthesis also necessarily unifies all interactions.

Originally, string theories were invented to describe only hadrons. When the spins (intrinsic angular momenta) of these particles are plotted as a function of the square of their mass, particles with the same properties (except mass and spin) lie on straight lines, called "Regge trajectories.'' According to quantum mechanics, spin can only take values which are integral or half-integral multiples of ħ (Planck's constant/2π), and there is a particle at each of these possible values, with mass given by the trajectory. Although the fact that hadrons are bound states implies the existence of such trajectories, the fact that the trajectories are linear implies the bound state can be approximated by a string consisting of quarks at the ends connected by a string of gluon flux. Since the quarks and gluons are never free, and the strings are a simpler description in some respects, it is sometimes more convenient to treat the hadrons directly as fundamental strings.

Unfortunately, certain quantum mechanical consistency conditions required that the known string theories include massless particles, whereas all observed hadrons are massive (and any massless hadrons would have been impossible to miss experimentally). On the other hand, there exist other particles which are massless, especially the graviton, photon, and gluons, and this suggested that these string theories be used instead to describe these fundamental particles, including the quarks and gluons from which the hadrons are made. However, the original motivation for string theories as describing Regge trajectories didn't apply to these fundamental strings: The mass scale of gravity (Planck's mass √ħc/G in terms of the speed of light c and the gravitational contant G) is so much larger (a factor of ≈10²⁰) than that of hadrons (the proton mass) that present-day accelerators are incapable of producing the massive particles occurring on the Regge trajectories of these fundamental strings. Fortunately, there is another motivation: The same quantum mechanical consistency conditions which prevented these string theories from describing hadrons also prevent non-string theories from describing gravity. This condition, "renormalizability,'' is concerned with infinities which may arise when summing over all possible configurations of particles exchanged in an interaction. Consistent string theories have no such infinities, and are thus capable of describing quantum gravity. A fascinating side-effect of this search for a theory of quantum gravity is the discovery of a theory which unifies all particles and forces: These same consistent string theories require not only the graviton but also other kinds of massless particles which can be identified with all the other known forces.

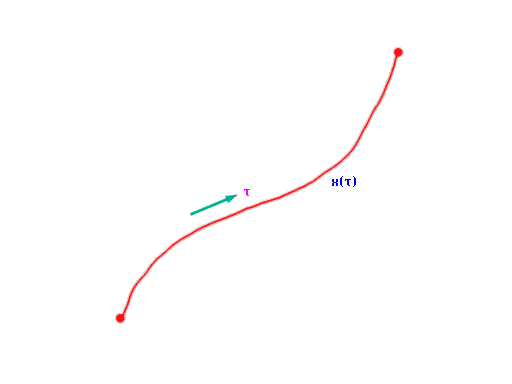
Before describing the string in more detail, we first review the particle. In relativistic theories time is like an extra coordinate of space. Space and time are then treated collectively as "spacetime,'' and vectors have a time component as well as the usual spatial components. The classical mechanics of the relativistic particle can be described in terms of an action which is just the proper length of the trajectory (world line) of the particle in spacetime:

S = -m∫√-dx², where dx² = d

→ x

² - dt² (in units c=1) and m is the "rest mass.'' The classical trajectory is then the shortest path between the given initial and final points in spacetime, corresponding to the minimum of this action: i.e., a straight line. In general, a curve through any kind of space can be described by writing all but one of the coordinates of any point on the curve as functions of the one remaining coordinate (in nonrelativistic theories, space as a function of time), or in a more symmetric way by writing all the coordinates in terms of some new parameter which varies arbitrarily along the curve: Unlike nonrelativistic mechanics, in relativistic mechanics there is an extra condition that the form of the action be independent of the choice of this parametrization. As a result, whereas in the nonrelativistic theory we find that the square of the spatial momentum is proportional to the energy, in the relativistic theory the square of the spacetime momentum is a constant, the square of the rest mass. This leads to the usual relativistic relation between the time component of the momentum (i.e., the energy) and the spatial components: p² =

→ p

² - E² = - m² .

Just as the particle, which is a zero-dimensional point in space, has a one-dimensional trajectory in spacetime, the string, which is a one-dimensional curve in space, sweeps out a two-dimensional surface in spacetime:

In analogy to the particle, a relativistic string is described by an action which is the area of this surface: S = -T∫√-(dX∧dX)²,
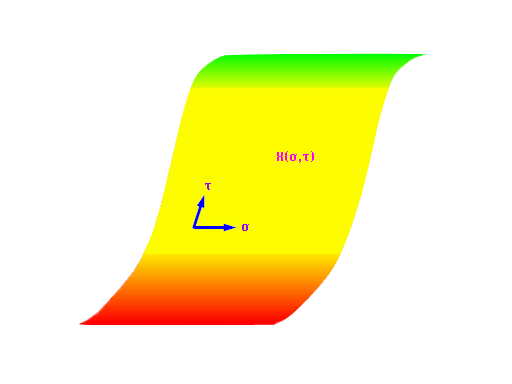
where T is the tension (and ∧ is the "wedge'' product, the generalization of the 3D vector cross product to arbitrary dimensions). The classical string thus sweeps out the surface with minimum area for the given initial and final string configurations. This surface is described by writing the coordinates as functions of two parameters. The condition that the form of the action be independent of the choice of these two parameters determines at each point along the string the contribution of that point to the string's energy in terms of that point's contribution to the spatial components of the momentum, and in terms of the vibrational mode of the string. The square of the total spacetime momentum of the string thus depends on the mode of excitation of the string, so different modes correspond to different particles with different rest masses. Thus, at any given τ, if we Fourier expand X(σ) in σ (running from 0 to π), with appropriate boundary conditions, X(σ) = x +

∞ ∑ n=1

x_n cos(nσ) ,
we can interpret the "average'' position x as the usual coordinate for a particle, and the x_n's are extra degrees of freedom on which the particle rest mass is found to depend.

Actually, there are a variety of particles and strings, of which the types we have just described are the simplest. In both cases, it's possible to introduce new physical degrees of freedom, besides the spacetime coordinates, which are also functions of the parameter(s) describing the trajectory (surface). In the case of the particle, these new degrees of freedom give the particle spin. In particular, certain choices introduce "supersymmetry,'' a symmetry which relates particles of integral spin ("bosons'') to particles of half-(odd)integral spin ("fermions''). For example, gluons (spin 1), photons (spin 1), and gravitons (spin 2) are bosons, while quarks (spin 1/2) and electrons (spin 1/2) are fermions, and supersymmetric particle theories have been proposed which would relate all these particles.

The simplest string already describes particles with spin (as mentioned above), since intrinsic angular momentum results from the parts of the string orbiting around its center. However, the resulting particles all have integral spin. Extra degrees of freedom now introduce half-integral spin. Furthermore, strings can be either open or closed curves in space (corresponding to sheets or tubes in spacetime):

Whereas open strings can describe massless particles of spin no greater than 1, closed strings always have a graviton. All string theories include closed strings, but not all include open ones. The string theory which is presently having the most success in describing the particles and forces observed in nature is a closed string theory where the vibrations traveling counterclockwise around the string have no extra degrees of freedom, while the clockwise ones do. (The two directions are distinguishable: We can label one direction by an arrow which tells the "orientation'' of the string.) This string has been dubbed the "heterotic'' string.

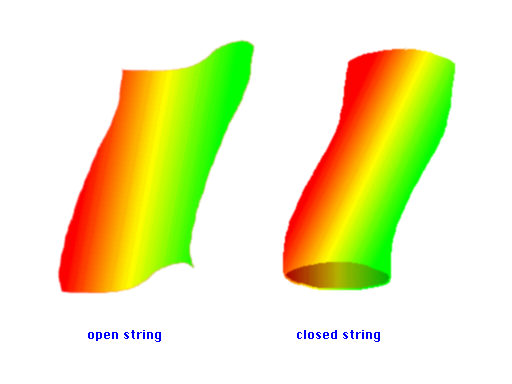
Although quantization of the particle is straightforward, consistency of the quantization of the string introduces a particularly unusual feature: The dimension of spacetime is determined to be 26 for the simplest string, and 10 or 2 for those with extra degrees of freedom. For various reasons (in particular, the lack of fermions and the presence of a tachyon, a particle with imaginary rest mass, or negative rest mass squared), the 26-dimensional string must be rejected. The 2-dimensional model has too few dimensions. Although the 10-dimensional theories would seem to have too many dimensions, this problem can be dealt with by a method known as "compactification'', whereby the 6 extra dimensions curl up into a ball so small that they can't be detected by present-day experiments. This compactification can be used to solve another problem: As mentioned above, the natural mass scale of strings which describe gravity is so large that the only presently observable particles are the massless ones. Thus, the string needs some dynamical mechanism by which to generate a new mass scale. The compactification may generate such a scale, if the shape into which the extra 6 dimensions shrink is asymmetric enough to accomodate more than one characteristic length (which is inversely related to a mass by ħ/c). Furthermore, this asymmetry may break another symmetry of 10-dimensional strings: All known quantum-consistent strings with fermions have supersymmetry, which is not observed (or at least badly broken) in nature. (Alternatively, all observed particles may be composites of the massless supersymmetric ones, with the required asymmetry coming from the binding mechanism.)

Just as a free string can be represented in spacetime as a sheet (or tube), interacting strings can be represented by surfaces of more complicated topologies:

For example, a sheet with a tear represents a string breaking into two strings. A sheet with a hole represents a string breaking into two strings which rejoin. This situation is simpler than the corresponding one for the particle, where interactions are described by lines intersecting in various ways. In particular, the action for interacting strings is still given by the area of a surface, where only the topology of the surface is fixed.

The fact that the action for interacting strings is independent of the parametrization of the surface (as well as being independent of the local scale of length in the surface in a certain sense) can be pictured by considering any two surfaces which can be deformed into one another by stretching the surface as being equivalent. (This stretching should be considered as a change in the choice of parameters in terms of which the string is described, and not as a change of the spacetime coordinates which are functions of these parameters.) For example, by such stretching any hole in the surface can be moved to any part of the surface. This stretchiness is sometimes called "duality,'' and manifests itself even in formalisms where the string interpretation of the theory is not obvious. For example, just as stretching the string surface can make interactions appear to change their order of occurence, so quantum mechanical amplitudes describing these interactions can be equally well described in terms of particles which interact in one order as in another, without considering both orderings. (This ordering is not an ordering in time, but rather an ordering with respect to how the world lines of the particles intersect.)

In summary, we see that string theory may not only provide the first consistent theory of quantum gravity, as well as a complete and realistic unification of gravity with all the other known particles and forces, but also suggests a completely new approach to that most fundamental area of science which was previously known as particle physics.