Reggeons meet partons

(CNYITP seminar, '05)

Oleg Andreev & Warren Siegel

hep-th/0410131

Quantized tension: Stringy amplitudes with Regge poles and parton behavior

Energy regions for hadrons

• Low: lattice, σ, instantons, nonrel. quarks
• Spectrum (high & low): Regge
• High, small angle (“soft”): Regge (sometimes pQCD)
• High, large angle (“hard”): pQCD

Regge theory

• α(t) relates spectrum & high-E, small-θ
• Spin J = α(M²), Amplitude ∼ β(t)s^α(t)
• “Small” coupling → α(t) = α’t + α₀ linear
• Tree = poles → DHS (s↔t) duality (strings)
• Experiment: OK for -2 GeV² ≤ t ≤ 6 GeV²;
  α’ ≈ 1 GeV^-2, α₀ ≈ ½ (ρ,ω,...)
• Reggeons (mesons/baryons) easier than pomerons (glueballs): spectrum known, cuts don’t get in way

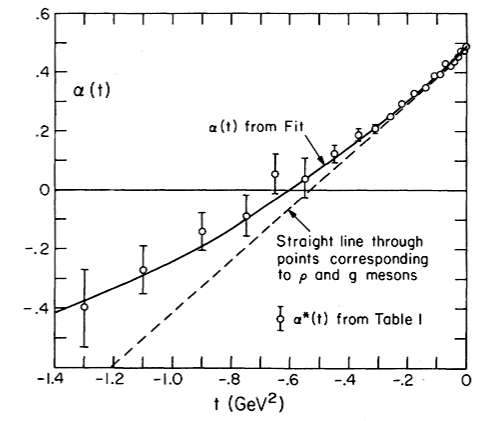
Barnes et al. ‘76 (Fermilab data)

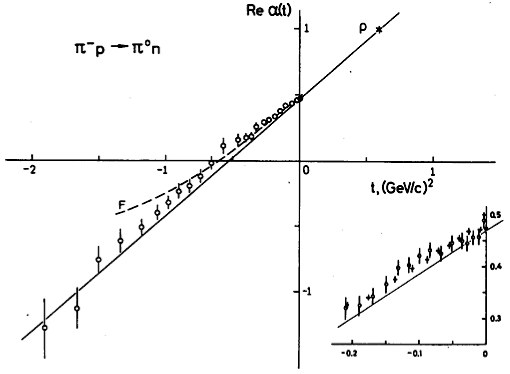
Apel et al. ‘79 (Serpukhov data)

t < 0: πN charge exchange scattering (t-channel pole)

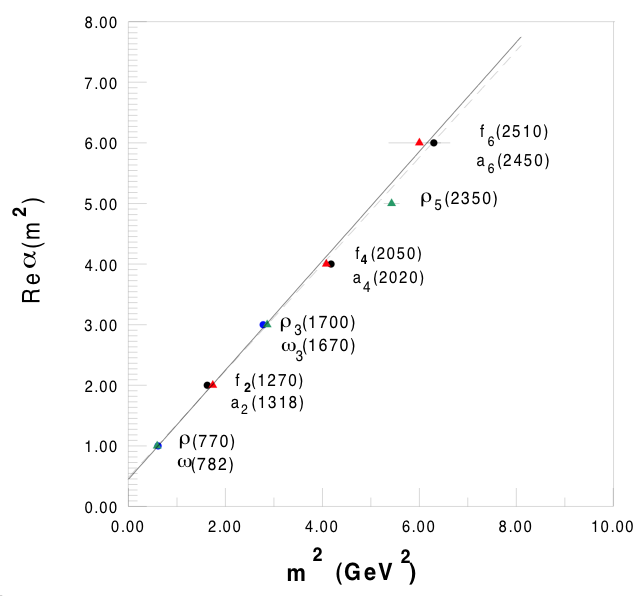
Desgrolard et al. ‘00 (PDG,RPP data)

t > 0: spectrum (s-channel pole)

Partons in Reggeons?

• Strings → exponentials, not powers, for parton propagators (large transverse p)
• pQCD = nonperturbative strings?
• Sum cuts or “sister trajectories”?
• How to interpolate small θ ↔ large θ?

AdS/CFT: Polchinski & Strassler

• AdS/CFT: 5th dimension = running tension
• P&S: α’ = cutoff on 5th D, introduces scale
• Continuum of trajectories, slope ≤ α’
• Regge & partons, but continuous spectrum

Continuum of trajectories → continuous spectrum (t > 0)

Our proposal

• ∑ over discrete tensions (not ∫ ) → discrete, integer-spaced spectrum
• Intercepts converge → partons
• Trees: leading order for both Reggeons & partons (cf. Gribov, Dokshitzer, Hoyer)

Cuts & sisters

• Quantized tension (OK)
• Higher tension only at higher-pt. → useful only for Pomeron (total cross section)
• Intercepts don’t converge → no partons
• Cuts: α_n(t) = α’t/n -bn +1
• Sisters: α_n(t) = (α’t+α₀)/n -½(n-1)

Picture

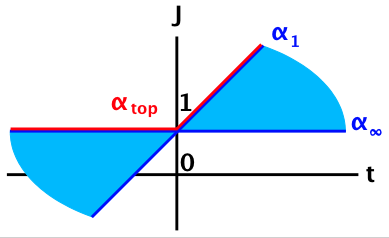
• Many (straight) trajectories α_n(t), but highest one (“top trajectory”) dominates
• For t > 0, α₁(t) = α’t+α₀ dominates → usual spectrum
• For -s ≪ t < 0, same or corrections from β_n(t) → still Regge (as for P-S)
• For t ≪ 0, α_∞(t) = const. dominates → usual parton behavior (as for P-S)

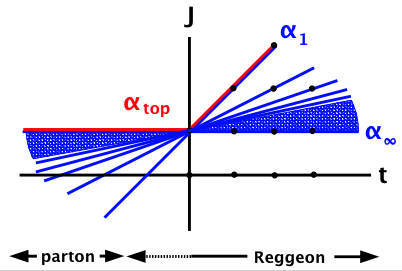
Corrections from weights extend Regge region to t < 0

General set-up

• α_n(t) has same poles as α₁(t) → α’M²+α₀ = a_n J + b_n ,
  a_n & b_n integers → α_n(t) = (α’t + α₀ - b_n)/a_n
• a_n & b_n increasing, b_n/a_n→ const. (n→∞)
• A = ∑w_nA_n , A_n = string amplitude, w_n ≈ (c/n)a_n^-c , c = ½ # quarks

Simplest model

• α_n(t) = α’(t-t₀)/n + J₀ , J₀ integer
• For t ≥ t₀, α_top(t) = α₁(t) = α’(t-t₀) +J₀
• For t ≤ t₀, α_top(t) = α_∞(t) = J₀
• With above w_n, A ∼ s^α₁(t) also for t₀ - t ≪ (c+1)/α’ln(α’s)
• Fixed θ, high E: A ∼ (α’s)^2-c (also more generally)

Interpretation

• Assume α_top(t) “turns” at t₀=0 (as for P-S),
  so α₁(t) = α’t +α₀, α_∞(t) = α₀
• α₀ ≈ ½ for Reggeon, 1 for Pomeron
• Then α_∞ (large -t) represents “jet” (far off-shell hadron), with α₀ = spin of parton carrying most of E (quark for Reggeon, gluon for Pomeron)
• So treat jet, not parton, as fundamental