1. INTRODUCTION
1.1. Motivation
The experiments which gave us quantum theory and general relativity are now quite old, but a satisfactory theory which is consistent with both of them has yet to be found. Although the importance of such a theory is undeniable, the urgency of finding it may not be so obvious, since the quantum effects of gravity are not yet accessible to experiment. However, recent progress in the problem has indicated that the restrictions imposed by quantum mechanics on a field theory of gravitation are so stringent as to require that it also be a unified theory of all interactions, and thus quantum gravity would lead to predictions for other interactions which can be subjected to present-day experiment. Such indications were given by supergravity theories [1.1], where finiteness was found at some higher-order loops as a consequence of supersymmetry, which requires the presence of matter fields whose quantum effects cancel the ultraviolet divergences of the graviton field. Thus, quantum consistency led to higher symmetry which in turn led to unification. However, even this symmetry was found insufficient to guarantee finiteness at all loops [1.2] (unless perhaps the graviton were found to be a bound-state of a truly finite theory). Interest then returned to theories which had already presented the possibility of consistent quantum gravity theories as a consequence of even larger (hidden) symmetries: theories of relativistic strings [1.3-5]. Strings thus offer a possibility of consistently describing all of nature. However, even if strings eventually turn out to disagree with nature, or to be too intractable to be useful for phenomenological applications, they are still the only consistent toy models of quantum gravity (especially for the theory of the graviton as a bound state), so their study will still be useful for discovering new properties of quantum gravity.The fundamental difference between a particle and a string is that a particle is a 0-dimensional object in space, with a 1-dimensional world-line describing its trajectory in spacetime, while a string is a (finite, open or closed) 1-dimensional object in space, which sweeps out a 2-dimensional world-sheet as it propagates through spacetime:
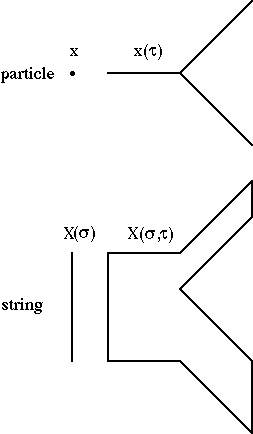
The nontrivial topology of the coordinates describes interactions. A string can be either open or closed, depending on whether it has 2 free ends (its boundary) or is a continuous ring (no boundary), respectively. The corresponding spacetime figure is then either a sheet or a tube (and their combinations, and topologically more complicated structures, when they interact).
Strings were originally intended to describe hadrons directly, since the observed spectrum and high-energy behavior of hadrons (linearly rising Regge trajectories, which in a perturbative framework implies the property of hadronic duality) seems realizable only in a string framework. After a quark structure for hadrons became generally accepted, it was shown that confinement would naturally lead to a string formulation of hadrons, since the topological expansion which follows from using 1/N_color as a perturbation parameter (the only dimensionless one in massless QCD, besides 1/N_flavor), after summation in the other parameter (the gluon coupling, which becomes the hadronic mass scale after dimensional transmutation), is the same perturbation expansion as occurs in theories of fundamental strings [1.6]. Certain string theories can thus be considered alternative and equivalent formulations of QCD, just as general field theories can be equivalently formulated either in terms of ``fundamental'' particles or in terms of the particles which arise as bound states. However, in practice certain criteria, in particular renormalizability, can be simply formulated only in one formalism: For example, QCD is easier to use than a theory where gluons are treated as bound states of self-interacting quarks, the latter being a nonrenormalizable theory which needs an unwieldy criterion (``asymptotic safety'' [1.7]) to restrict the available infinite number of couplings to a finite subset. On the other hand, atomic physics is easier to use as a theory of electrons, nuclei, and photons than a formulation in terms of fields describing self-interacting atoms whose excitations lie on Regge trajectories (particularly since QED is not confining). Thus, the choice of formulation is dependent on the dynamics of the particular theory, and perhaps even on the region in momentum space for that particular application: perhaps quarks for large transverse momenta and strings for small. In particular, the running of the gluon coupling may lead to nonrenormalizability problems for small transverse momenta [1.8] (where an infinite number of arbitrary couplings may show up as nonperturbative vacuum values of operators of arbitrarily high dimension), and thus QCD may be best considered as an effective theory at large transverse momenta (in the same way as a perturbatively nonrenormalizable theory at low energies, like the Fermi theory of weak interactions, unless asymptotic safety is applied). Hence, a string formulation, where mesons are the fundamental fields (and baryons appear as skyrmeon-type solitons [1.9]) may be unavoidable. Thus, strings may be important for hadronic physics as well as for gravity and unified theories; however, the presently known string models seem to apply only to the latter, since they contain massless particles and have (maximum) spacetime dimension D = 10 (whereas confinement in QCD occurs for D ≤ 4).
1.2. Known models (interacting)
Although many string theories have been invented which are consistent at the tree level, most have problems at the one-loop level. (There are also theories which are already so complicated at the free level that the interacting theories have been too difficult to formulate to test at the one-loop level, and these will not be discussed here.) These one-loop problems generally show up as anomalies. It turns out that the anomaly-free theories are exactly the ones which are finite. Generally, topological arguments based on reparametrization invariance (the ``stretchiness'' of the string world sheet) show that any multiloop string graph can be represented as a tree graph with many one-loop insertions [1.10], so all divergences should be representable as just one-loop divergences. The fact that one-loop divergences should generate overlapping divergences then implies that one-loop divergences cause anomalies in reparametrization invariance, since the resultant multi-loop divergences are in conflict with the one-loop-insertion structure implied by the invariance. Therefore, finiteness should be a necessary requirement for string theories (even purely bosonic ones) in order to avoid anomalies in reparametrization invariance. Furthermore, the absence of anomalies in such global transformations determines the dimension of spacetime, which in all known nonanomalous theories is D=10. (This is also known as the ``critical,'' or maximum, dimension, since some of the dimensions can be compactified or otherwise made unobservable, although the number of degrees of freedom is unchanged.)In fact, there are only four such theories:
I: N=1 supersymmetry, SO(32) gauge group, open [1.11] IIA,B: N=2 nonchiral or chiral supersymmetry [1.12] heterotic: N=1 supersymmetry, SO(32) or E(8) E(8) [1.13]
or broken N=1 supersymmetry, SO(16) SO(16) [1.14]
All except the first describe only closed strings; the first describes open strings, which produce closed strings as bound states. (There are also many cases of each of these theories due to the various possibilities for compactification of the extra dimensions onto tori or other manifolds, including some which have tachyons.) However, for simplicity we will first consider certain inconsistent theories: the bosonic string, which has global reparametrization anomalies unless D=26 (and for which the local anomalies described above even for D=26 have not yet been explicitly derived), and the spinning string, which is nonanomalous only when it is truncated to the above strings. The heterotic strings are actually closed strings for which modes propagating in the clockwise direction are nonsupersymmetric and 26-dimensional, while the counterclockwise ones are N=1 (perhaps-broken) supersymmetric and 10-dimensional, or vice versa.
1.3. Aspects
There are several aspects of, or approaches to, string theory which can best be classified by the spacetime dimension in which they work: D = 2, 4, 6, 10. The 2D approach is the method of first-quantization in the two-dimensional world sheet swept out by the string as it propagates, and is applicable solely to (second-quantized) perturbation theory, for which it is the only tractable method of calculation. Since it discusses only the properties of individual graphs, it can't discuss properties which involve an unfixed number of string fields: gauge transformations, spontaneous symmetry breaking, semiclassical solutions to the string field equations, etc. Also, it can describe only the gauge-fixed theory, and only in a limited set of gauges. (However, by introducing external particle fields, a limited amount of information on the gauge-invariant theory can be obtained.) Recently most of the effort in this area has been concentrated on applying this approach to higher loops. However, in particle field theory, particularly for Yang-Mills, gravity, and supersymmetric theories (all of which are contained in various string theories), significant (and sometimes indispensable) improvements in higher-loop calculations have required techniques using the gauge-invariant field theory action. Since such techniques, whose string versions have not yet been derived, could drastically affect the S-matrix techniques of the 2D approach, we do not give the most recent details of the 2D approach here, but some of the basic ideas, and the ones we suspect most likely to survive future reformulations, will be described in chapters 6-9.The 4D approach is concerned with the phenomenological applications of the low-energy effective theories obtained from the string theory. Since these theories are still very tentative (and still too ambiguous for many applications), they will not be discussed here. (See [1.15,0.1].)
The 6D approach describes the compactifications (or equivalent
eliminations) of the 6 additional dimensions which must shrink from
sight in order to obtain the observed dimensionality of the macroscopic
world. Unfortunately, this approach has several problems which inhibit
a useful treatment in a book: (1) So far, no justification has been
given as to why the compactification occurs to the desired models, or to
4 dimensions, or at all; (2) the style of compactification
(Kal
What is discussed here is primarily the 10D approach, or second quantization, which seeks to obtain a more systematic understanding of string theory that would allow treatment of nonperturbative as well as perturbative aspects, and describe the enlarged hidden gauge symmetries which give string theories their finiteness and other unusual properties. In particular, it would be desirable to have a formalism in which all the symmetries (gauge, Lorentz, spacetime supersymmetry) are manifest, finiteness follows from simple power-counting rules, and all possible models (including possible 4D models whose existence is implied by the 1/N expansion of QCD and hadronic duality) can be straightforwardly classified. In ordinary (particle) supersymmetric field theories [1.17], such a formalism ( superfields or superspace) has resulted in much simpler rules for constructing general actions, calculating quantum corrections ( supergraphs), and explaining all finiteness properties (independent from, but verified by, explicit supergraph calculations). The finiteness results make use of the background field gauge, which can be defined only in a field theory formulation where all symmetries are manifest, and in this gauge divergence cancellations are automatic, requiring no explicit evaluation of integrals.
1.4. Outline
String theory can be considered a particular kind of particle theory, in that its modes of excitation correspond to different particles. All these particles, which differ in spin and other quantum numbers, are related by a symmetry which reflects the properties of the string. As discussed above, quantum field theory is the most complete framework within which to study the properties of particles. Not only is this framework not yet well understood for strings, but the study of string field theory has brought attention to aspects which are not well understood even for general types of particles. (This is another respect in which the study of strings resembles the study of supersymmetry.) We therefore devote chapts. 2-4 to a general study of field theory. Rather than trying to describe strings in the language of old quantum field theory, we recast the formalism of field theory in a mold prescribed by techniques learned from the study of strings. This language clarifies the relationship between physical states and gauge degrees of freedom, as well as giving a general and straightforward method for writing free actions for arbitrary theories.In chapts. 5-6 we discuss the mechanics of the particle and string. As mentioned above, this approach is a useful calculational tool for evaluating graphs in perturbation theory, including the interaction vertices themselves. The quantum mechanics of the string is developed in chapts. 7-8, but it is primarily discussed directly as an operator algebra for the field theory, although it follows from quantization of the classical mechanics of the previous chapter, and vice versa. In general, the procedure of first-quantization of a relativistic system serves only to identify its constraint algebra, which directly corresponds to both the field equations and gauge transformations of the free field theory. However, as described in chapts. 2-4, such a first-quantization procedure does not exist for general particle theories, but the constraint system can be derived by other means. The free gauge-covariant theory then follows in a straightforward way. String perturbation theory is discussed in chapt. 9.
Finally, the methods of chapts. 2-4 are applied to strings in chapts. 10-12, where string field theory is discussed. These chapters are still rather introductory, since many problems still remain in formulating interacting string field theory, even in the light-cone formalism. However, a more complete understanding of the extension of the methods of chapts. 2-4 to just particle field theory should help in the understanding of strings.
Chapts. 2-5 can be considered almost as an independent book, an attempt at a general approach to all of field theory. For those few high energy physicists who are not intensely interested in strings (or do not have high enough energy to study them), it can be read as a new introduction to ordinary field theory, although familiarity with quantum field theory as it is usually taught is assumed. Strings can then be left for later as an example. On the other hand, for those who want just a brief introduction to strings, a straightforward, though less elegant, treatment can be found via the light cone in chapts. 6,7,9,10 (with perhaps some help from sects. 2.1 and 2.5). These chapters overlap with most other treatments of string theory. The remainder of the book (chapts. 8,11,12) is basically the synthesis of these two topics.
REFERENCES
Preface
- 0.1
- M.B. Green, J.H. Schwarz, and E. Witten, Superstring theory, v. 1-2 (Cambridge University, Cambridge, 1987).
- 0.2
- V. Gates, E. Kangaroo, M. Roachcock, and W.C. Gall,
The super G-string, in Unified string theories,
eds. M. Green and D. Gross, Proc. of Santa Barbara Workshop,
Jul. 29 - Aug. 16, 1985 (World Scientific, Singapore, 1986) p. 729;
Super G-string field theory, in Superstrings, Cosmology and Composite Structures, eds. S.J. Gates, Jr. and R.N. Mohapatra, Proc. of International Workshop on Superstrings, Composite Structures, and Cosmology, College Park, MD, March 11-18, 1987 (World Scientific, Singapore, 1987) p. 585.
Chapter 1
- 1.1
- P. van Nieuwenhuizen, Phys. Rep. 68 (1981) 189.
- 1.2
- M.T. Grisaru and W. Siegel, Nucl.Phys. B 201 (1982) 292, B206 (1982) 496;
N. Marcus and A. Sagnotti, Phys.Lett. 135B (1984) 85;
M.H. Goroff and A. Sagnotti, Phys.Lett. 160B (1985) 81. - 1.3
- Dual theory, ed. M. Jacob (North-Holland, Amsterdam, 1974);
J. Scherk, Rev. Mod. Phys. 47 (1975) 123;
P.H. Frampton, Dual resonance models and string theories (World Scientific, Singapore, 1986). - 1.4
- S. Mandelstam, Phys. Rep. 13 (1974) 259.
- 1.5
- J.H. Schwarz, Phys. Rep. 89 (1982) 223.
- 1.6
- G. 't Hooft, Nucl.Phys. B 72 (1974) 461.
- 1.7
- S. Weinberg, Critical phenomena for field theorists,
in Understanding the fundamental constituents of matter,
proc. of the International School of Subnuclear Physics, Erice, 1976,
ed. A. Zichichi (Plenum, New York, 1978) p. 1;
Ultraviolet divergences in quantum theories of gravitation, in General relativity: an Einstein centenary survey, eds. S.W. Hawking and W. Israel (Cambridge University, Cambridge, 1979) p. 790. - 1.8
- G. 't Hooft, Phys.Lett. 109B (1982) 474.
- 1.9
- T.H.R. Skyrme, Proc. Roy. Soc. A260 (1961) 227;
E. Witten, Nucl.Phys. B 223 (1983) 433. - 1.10
- D.J. Gross, A. Neveu, J. Scherk, and J.H. Schwarz, Phys.Lett. 31B (1970) 592.
- 1.11
- M.B. Green and J.H. Schwarz, Phys.Lett. 149B (1984) 117.
- 1.12
- M.B. Green and J.H.Schwarz, Phys.Lett. 109B (1982) 444.
- 1.13
- D.J. Gross, J.A. Harvey, E. Martinec, and R. Rohm, Phys.Rev.Lett. 54 (1985) 502, Nucl.Phys. B 256 (1985) 253, Nucl.Phys. B 267 (1986) 75.
- 1.14
- L.J. Dixon and J.A. Harvey, Nucl.Phys. B 274 (1986) 93;
L. Alvarez-Gaumé, P. Ginsparg, G. Moore, and C. Vafa, Phys.Lett. 171B (1986) 155;
H. Itoyama and T.R. Taylor, Phys.Lett. 186B (1987) 129. - 1.15
- E. Witten, Phys.Lett. 149B (1984) 351.
- 1.16
- P. Candelas, G.T. Horowitz, A. Strominger, and E. Witten, Nucl.Phys. B
258 (1985) 46;
L. Dixon, J.A. Harvey, C. Vafa, and E. Witten, Nucl.Phys. B 261 (1985) 678, 274 (1986) 285;
K.S. Narain, Phys.Lett. 169B (1986) 41;
H. Kawai, D.C. Lewellen, and S.-H.H. Tye, Nucl.Phys. B 288 (1987) 1;
I. Antoniadis, C. Bachas, and C. Kounnas, Nucl.Phys. B 289 (1987) 87;
R. Bluhm, L. Dolan, and P. Goddard, Nucl.Phys. B 289 (1987) 364, Unitarity and modular invariance as constraints on four-dimensional superstrings, Rockefeller preprint RU87/B1/25 DAMTP 88/9 (Jan. 1988). - 1.17
- S.J. Gates, Jr., M.T. Grisaru, M. Rocek, and W. Siegel,
Superspace, or One thousand and one lessons in supersymmetry
(Benjamin/Cummings, Reading, 1983);
J. Wess and J. Bagger, Supersymmetry and supergravity (Princeton University, Princeton, 1983);
R.N. Mohapatra, Unification and supersymmetry: the frontiers of quark-lepton physics (Springer-Verlag, New York, 1986);
P. West, Introduction to supersymmetry and supergravity (World Scientific, Singapore, 1986).
