The Ising model is a two dimensional collection of classical ``spins''
![]() which take on the two values +1 and -1 and are located
at the j row and k column of a square lattice. For a
translationally invariant system the interaction energy of this system
is
which take on the two values +1 and -1 and are located
at the j row and k column of a square lattice. For a
translationally invariant system the interaction energy of this system
is
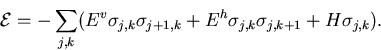 |
(1) |
In 1966 I began my long involvement with this model when, for part of my thesis, Prof. Wu suggested that I compute for an Ising model on a half plane the same quantities which Onsager and Yang computed for the bulk. At the time we both thought that because the presence of the boundary breaks translational invariance the boundary computations would be at least as difficult as the bulk computations. It was therefore quite surprising when it turned out that the computations were drastically simpler [3]. In the first place the model could be solved in the presence of a field on the boundary which meant that the computation of the magnetization came along for free once we could do the free energy but more importantly the correlation functions, which in the bulk were given by large determinants whose size increased with the separation of the spins, were here given by nothing worse than the product of two one dimensional integrals for all separations. The key to this great simplification is the fact that the extra complication of the boundary magnetic field actually makes the problem simpler to solve (a realization I had in a dream at 3:00 AM after a New Years eve party).
This model is the first case where boundary critical exponents were explicitly computed. Indeed it remained almost the only solved problem of a boundary critical phenomena until the invention of boundary conformal field theory in 1993 [4].
This boundary field had the added virtue that we could analytically continue the boundary magnetization into the metastable region and explicitly compute a boundary hysteresis effect [5]. This leads to the lovely effect that near the value of the boundary magnetic field where the hysteresis curve ends that the spins a very long distance from the boundary turn over from pointing in the direction of the bulk magnetization to pointing in the direction of the metastable surface spin. At the value where the metastability ends this surface effect penetrates all the way to infinity and ``flips'' the spin in the bulk. In later years this phenomena has been interpreted at a ``wetting transition'' [6] and the Ising intuition has been extended to many models where exact solutions do not exist.