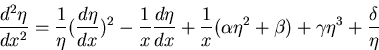Next: Ising model in a
Up: The Ising Model
Previous: Random layered Ising model
But perhaps the most dramatic discoveries were
published from 1973 to 1981 on the
spin correlation functions of the Ising model and most particularly the
results that in the scaling limit where 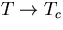 and the
separation of the spins
and the
separation of the spins 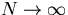 such that |T-Tc|N=r
is fixed that the correlation function [14]
such that |T-Tc|N=r
is fixed that the correlation function [14]
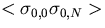 divided by |T-Tc|1/4 is
divided by |T-Tc|1/4 is
| ![\begin{displaymath}
G_{\pm}(2r)=(1\mp\eta)\eta^{-1/2}{\rm exp}\int_r^{\infty}dx{1\over
4}x\eta^{-2}[(1-\eta^2)^2-\eta'^2]\end{displaymath}](img6.gif) |
(2) |
where 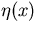 satisfies the third equation of Painlevé [15]
satisfies the third equation of Painlevé [15]
| 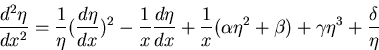 |
(3) |
with 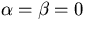 and
and 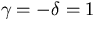 and
and
| 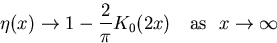 |
(4) |
where K0(2x) is the modified Bessel function of order zero.
Furthermore on the lattice all the correlation functions satisfy
quadratic difference equations [16].
This discovery of Painlevé equations in the Ising model was the
beginning of a host of developments in mathematical physics which
continues in an ever expanding volume to this day. It lead Sato, Miwa,
and Jimbo [17] to their celebrated series of work on isomonodromic
deformation and to the solution of the distribution of eigenvalue of
the GUE random matrix problem [18] in terms of a Painlevé V
function. This has subsequently been extended by many people, including
one of our original collaborators, Craig Tracy [19],
to so many branches of
physics and mathematics including random matrix theory matrix models
in quantum gravity and random permutations that entire semester long
work shops are now devoted to the subject. Indeed a recent book on
special functions [20] characterized
Painlevé functions and ''the special
functions of the 21st century.'' Rarely has the solution to one
small problem in physics had so many ramifications in so many
different fields.



Next: Ising model in a
Up: The Ising Model
Previous: Random layered Ising model
Barry McCoy
3/29/1999
![]() and the
separation of the spins
and the
separation of the spins ![]() such that |T-Tc|N=r
is fixed that the correlation function [14]
such that |T-Tc|N=r
is fixed that the correlation function [14]
![]() divided by |T-Tc|1/4 is
divided by |T-Tc|1/4 is