Particles
Many physics majors who plan to do research in grad school on high energy
physics have little or no knowledge on the subject, having read articles
or books written for people with only a high-school education in physics
(or less). (I have no clue why.) Most such physics falls under the
geometrical headings of "particles" or
"strings".
Symmetries
There are various kinds of symmetries in particle physics. In particular, there are local symmetries, which have independent transformations at each point in spacetime, and global symmetries, which transform the same way everywhere. There are also spacetime symmetries, which act on coordinates, and internal symmetries, which don't.| global | local | |
|---|---|---|
| spacetime |
special relativity: Poincaré (Lorentz, translations) |
general relativity: arbitrary coordinates |
| internal |
approximate: flavor (isospin, etc.) |
gauge: color, electroweak |
Relativity
Special relativity, simply stated (more simply than by rotations, Lorentz transformations, etc.), is the symmetry that leaves invariant the infinitesimal distance element (proper time) ds:as a generalization of the nonrelativistic distance element given by just the last 3 terms, a generalization of the Pythagorean theorem. (We use units c=1.) General relativity uses arbitrary coordinates, describing curved space.
Isospin
Internal symmetries relate similar types of particles. For example, isospin relates protons and neutrons, which have the same spin, and about the same mass, but different charge. The proton and neutron form a doublet that transform into each other, in the same way as the 2 spin states of a spin 1/2 particle, hence the name "iso(topic)spin". (Nuclei that differ by exchanges of protons and neutrons form different isotopes of the same "isobar".) In that sense, they are 2 isospin states of a single type of particle, the "nucleon". Both spin (actually rotations) and isospin transformations are examples of the group "SU(2)".Flavor
Things will stay simpler if we work in terms of quarks instead of hadrons. Then the "up" and "down" quarks that make up the neutron and proton also form a doublet of SU(2) isospin (and each one is a doublet of SU(2) spin, again just like the nucleons), These 2 quarks, like the 2 nucleons, are very close in mass, so this SU(2) symmetry is very accurate. There is a third quark, the "strange" quark, that is somewhat more different in mass. These 3 quarks together form a triplet of a bigger group, "SU(3)", that juggles all 3 among themselves. Thus, SU(3) transformations include SU(2) as a "subgroup". But there are even more quarks (at least 6 total), which differ greatly in mass, giving an "SU(6)" symmetry, which is very poor, at least as far as relating masses. So basically SU(N) is just the symmetry that says you have N different "flavors" of quarks that act pretty much the same way, at least with respect to the strong interactions, except for their masses.Electromagnetism
But the quarks have different charges, because they interact differently with respect to the electromagnetic (and also weak) interactions. Electromagnetism is described by a "U(1)" symmetry, because it can relate a single particle to itself, by multiplying its wave function by a phase. (SU(N) is the same as U(N) less a U(1). For the above SU(N)'s, that U(1) symmetry is associated with "baryon number", which is 1 for baryons like the nucleon, 1/3 for each of the 3 quarks that make up a baryon, -1/3 for an antiquark, 0 for a meson made of a quark and antiquark, etc.)Weak interactions
This U(1) symmetry associated with charge is a local symmetry because the coupling of the spin-1 photon of electromagnetism couples to its current (a local quantity, the distribution of charge). Similarly, the weak interactions responsible for the slower particle decays is described by a local SU(2) symmetry, mediated by the W+, W-, and Z bosons (a triplet of this SU(2), and also each a triplet of spin SU(2)) and the Higgs. (Actually the photon and Z are mixtures of the U(1) particle and 1 of the 3 SU(2) particles, because of the way the Z and W's get mass.)Strong interactions
Finally, the strong interactions are mediated by the spin-1 gluons of an SU(3) symmetry that bind quarks (and themselves) together. There are thus 3 "colors" of quarks (besides their 6 "flavors"), but we never see the colors because they cancel in their bound states, the hadrons (baryons, antibaryons, and mesons). The leptons (electron, muon, tauon, and their neutrinos) also come in 6 flavors, but no colors, so they interact only electroweakly, not strongly, and are not confined. (You can take the electron out of the atom, but you can't take the quark out of the proton.)Dynamics
The most important calculational tool in particle physics is perturbation theory, because it gives a systematic expansion of exact results that are often accurate already at lowest order, and can be improved at higher orders. This expansion is represented by "Feynman diagrams", pretty pictures that actually have mathematical significance. These "graphs" take the place of equations that would be much longer and harder to express as a 1-dimensional line of text. Each such graph is associated with a quantum mechanical amplitude describing a specific scattering process.
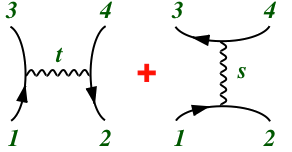
Propagators
The diagram consists of various lines (segments), representing the paths of free particles (waves). They can be solid or dashed, straight, wavy, or curly, indicating different types of particles. They can even be multiple parallel lines, indicating the quarks that make up a hadron. Each line is assigned a momentum, so the particle is actually a plane wave; as usual, arbitrary states can be represented as superpositions. Each line is then associated with a "propagator" ("Green function", "kernel"), as is always used when giving the general solution of a free (differential) wave equation. When working with momentum eigenstates (by Fourier transformation), propagators are just rational functions of momenta. When the particles carry spin or internal symmetry, there are also indices associated with the propagator indicating the corresponding state.Vertices
These line segments begin and end at "vertices". These intersections describe the collisions of these particles at points, where particles may also be created or annihilated. The pointlike nature of these collisions is enforced by momentum conservation at the vertex, and the association of each vertex with a polynomial (usually just linear) in the momenta of the colliding particles, as well as numerical factors associated with spin and internal symmetry, and a coupling constant.External lines
Finally, there are also short line segments coming out of some vertices with the other ends free. Each free end is associated with the wave function of an initial single-particle state, or the complex conjugate of a final one. As with the propagators, each of these lines is assigned a momentum and spin/internal symmetry numbers specifying that state.Loops
Putting together all the factors from propagators, vertices, and external line factors, we get some function of momenta, the probability amplitude for that process. Some "internal" momenta of the propagators are determined by the "external" momenta of the wave functions (and similarly for spin and internal symmetry by their conservation or interaction-specified breaking). If there are closed "loops" in the graph, for each there is a corresponding undetermined momentum, which must then be integrated over to get the contribution from all possible internal states (and the corresponding spin and internal symmetry states must be summed over).
