Condensed matter (including cold atoms):
1. With
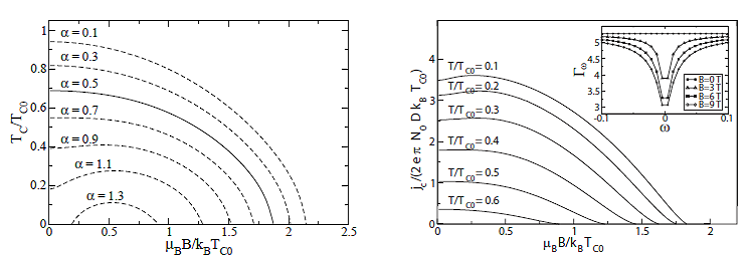
my collaborators, I developed a theory of superconductors with magnetic
impurities in the presence of magnetic field to predict anomalous behavior of
superconductivity and successfully explained the critical current data from
Bezryadin’s group.

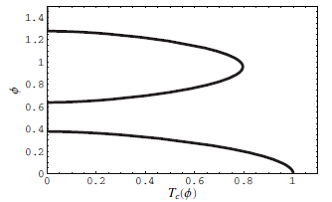
2. I
studied the Little-Parks effect in small superconducting rings and predicted an
additional single-particle period of h/e in addition to h/2e. Furthermore, we
sketched possible scenarios of superconducting-normal transitions. We have
found qualitative agreement of our theory and the experiments on
superconducting hollow cylinders done in Liu’s group in PennState.
3. I
investigated the critical velocity in one-dimensional superconductor. We have
found that the transition to normal state is not what was thought previously,
but of different nature. Among other things, we corrected an error in the
literature of critical velocity in one dimension.

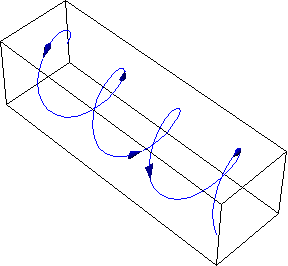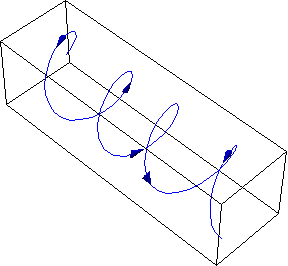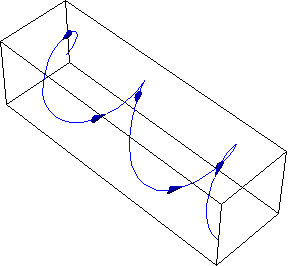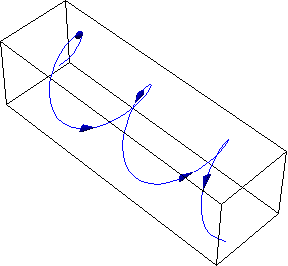
4. Together
with Bezryadin’s experimental group, we studied possible probes of superfluid
density and vortex motion. We also studied phase slips (possibly quantum) via
switching current fluctuations, and the experiments had shown strong evidence
of quantum phase slips.
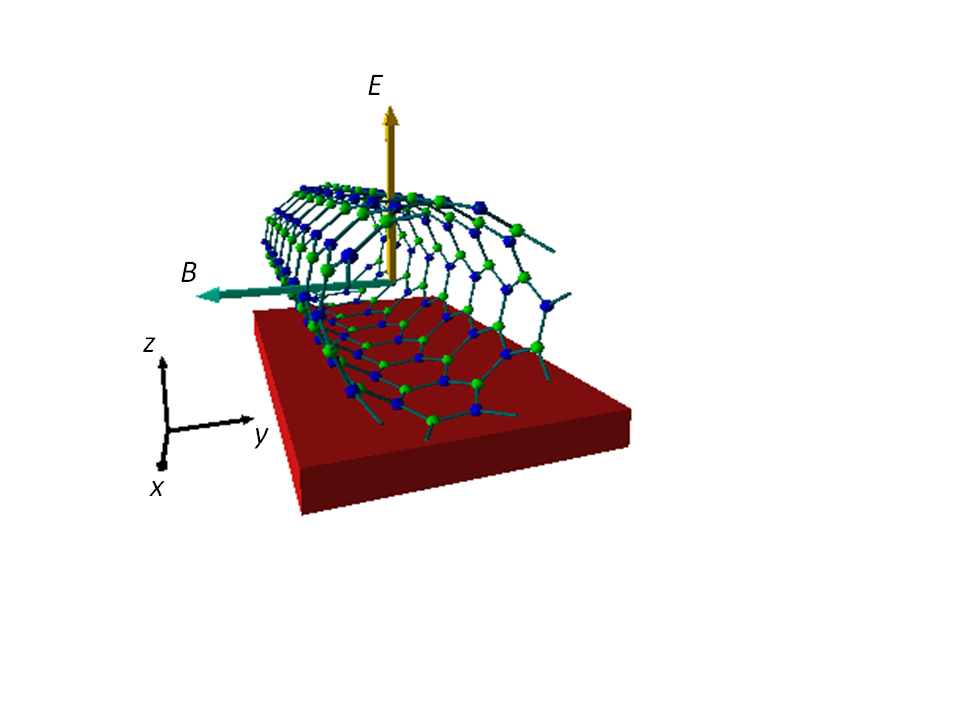
5. My
collaborators and I studied the nanotube quantum dots and the effect of
transverse fields on nanotubes. We found a continuous gap opening and breakings
of valley, particle-hole, and left-right-moving degeneracies. We also
investigated how the interaction was modified by fields and how the
Luttinger-liquid behavior was modified. In particular, a possible
charge-spin-band separation phenomenon can occur.
6. My
collaborators and I studied Bose gas in optical lattices. We have
accounted for
the inhomogeneous superfluid and Mott structures and provided a simple
counting
recipe for creating Mott states that may be potentially useful in
quantum
information processing using cold atoms. The groups of I. Bloch and of
W. Ketterle had separately implemented schemes similar to our proposed
scheme.

7. We
have also investigated collective modes and dynamics of superfluids in novel
geometries such as a bubble trap. In particular, we studied the expansion of a
Bose condensate in a shell trap, which results in an interesting
self-interference and a seemingly shock wave.
Quantum information:
1. We
developed a theory for quantifying multipartite (many-body) entanglement. First
we showed that this measure is an entanglement monotone, namely, a good
entanglement measure. We bench-marked this measure against both pure and mixed
quantum states appearing in quantum information. More importantly, we also applied
this measure to ground states in quantum phase transitions, and found
connection of the divergence in entanglement to critical points.
2. Recently, I have also connected the notion of entanglement to the notion of renormalization group transformation on states and applied the merging of these two notions to the study of two spin models (spin ½ and 1, respectively) with quantum phase transitions. A generic picture of the behavior of entanglement (and under RG) has emerged, which results from a scaling hypothesis of entanglement.
3. With my collaborators, I have also studied other entanglement measures and the connection to one another. In particular, I have proved an analytic formula for evaluating the relative entropy of entanglement (which is a multipartite entanglement measure that is generally difficult to calculate) for certain mixture of symmetric states.
4. Motivated by the discussions with P. Kwiat’s experimental quantum-optics group, I developed schemes for generating and manipulating arbitrary two-photon polarization states. This work provides a positive answer to a question raised earlier by people working on entangled photons: is it possible to create arbitrary two-photon entangled states described by valid density matrices? These schemes later enabled many experiments in quantum information processing protocols, including quantum process tomography, tests of Bell-inequalities (including Collins-Gisin inequality) via both pure and mixed states, remote state preparation, and quantum orienteering.
5. With J. Barreiro and P. Kwiat, I also analyzed theoretically the limit of hyper-entanglement in, e.g., Bell-state analysis and its application to dense coding, teleportation and quantum fingerprinting. We also broke the limit of channel capacity 1.58 of linear optics, using hyper-entanglement.
6. With M. Mosca and A. Nayak, I have examined the computational complexity of bosonic systems. To our surprise, we found that bosonic problems, such as solving the ground state energy of interacting bosons and the bosonic version of the N-representability problem, can indeed be so hard that even quantum computers (if we have) are not likely to solve them efficiently.
7. Continuing
the quest of entanglement theory, I have also established a connection of
entanglement to permanent (with