


Next: Beyond Integrability
Up: From Ising to integrable
Previous: The chiral Potts model
One particularly important property of integrable systems is seen in
the spectrum of excitations above the ground state. In all known cases
these spectra is of the quasi particle form in which the energies of
multiparticle states is additively composed of single particle
energies 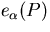
| 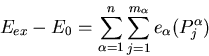 |
(10) |
with the total momentum
| 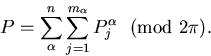 |
(11) |
Here n is the number of types of quasi-particles and there are
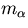 quasi particles of type
quasi particles of type 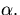 The momenta in the allowed states are
quantized in
units of
The momenta in the allowed states are
quantized in
units of 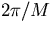 and are chosen from the sets
and are chosen from the sets
| 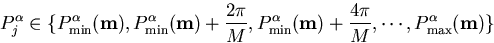 |
(12) |
with the Fermi exclusion rule
| 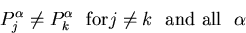 |
(13) |
and
| 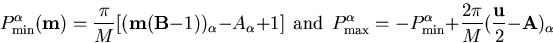 |
(14) |
where if some 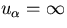 the corresponding
the corresponding
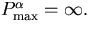
If some 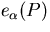 vanishes at some momentum (say 0) the system
is massless and for
vanishes at some momentum (say 0) the system
is massless and for 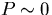 a typical behavior is
a typical behavior is 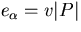 where v is variously called the speed of light or sound or the
spin wave velocity.
where v is variously called the speed of light or sound or the
spin wave velocity.
The important feature of the momentum selection rules (12) is
that in addition to the fermionic exclusion rule (13) is the
exclusion of a certain number of momenta at the edge of the momentum zones
which is proportional to the number of quasiparticles in the state.
For the Ising model at zero field there is only one quasi particle
and 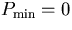 so the quasiparticle is exactly the same as a free
fermion. However, for all other cases the
so the quasiparticle is exactly the same as a free
fermion. However, for all other cases the  is not zero
and exclusion does indeed take place. This is a very explicit
characterization of the generalization which general integrable models
make over the Ising model.
is not zero
and exclusion does indeed take place. This is a very explicit
characterization of the generalization which general integrable models
make over the Ising model.
The exclusion rules (12) lead to what have been called fractional
(or exclusion) statistics by Haldane [36].
On the other hand they make a remarkable and beautiful
connection with the mathematical theory of Rogers-Ramanujan
identities and conformal field theory. We have found that these
exclusion rules allow a reinterpretation of all conformal field
theories (which are usually discussed in terms of a bosonic Fock space
using a Feigen and Fuchs construction [37]) in terms of a
set of fermionic quasi-particles [38]. What is most surprising
is that there is not just one fermionic representation for each
conformal field theory but there are at least as many distinct
fermionic representations as thee are integrable perturbations. The
search for the complete set of fermionic representations is ongoing
and I will only mention here that we have extensive results for the
integrable perturbations of the minimal models M(p,p') for the
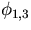 perturbation [39] and the
perturbation [39] and the 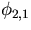 and
and
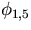 perturbations [40].
perturbations [40].



Next: Beyond Integrability
Up: From Ising to integrable
Previous: The chiral Potts model
Barry McCoy
3/29/1999
![]()
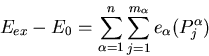
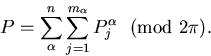
![]() vanishes at some momentum (say 0) the system
is massless and for
vanishes at some momentum (say 0) the system
is massless and for ![]() a typical behavior is
a typical behavior is ![]() where v is variously called the speed of light or sound or the
spin wave velocity.
where v is variously called the speed of light or sound or the
spin wave velocity.
![]() so the quasiparticle is exactly the same as a free
fermion. However, for all other cases the
so the quasiparticle is exactly the same as a free
fermion. However, for all other cases the ![]() is not zero
and exclusion does indeed take place. This is a very explicit
characterization of the generalization which general integrable models
make over the Ising model.
is not zero
and exclusion does indeed take place. This is a very explicit
characterization of the generalization which general integrable models
make over the Ising model.
![]() perturbation [39] and the
perturbation [39] and the ![]() and
and
![]() perturbations [40].
perturbations [40].