


Next: Exclusion statistics and Rogers-Ramanujan
Up: From Ising to integrable
Previous: From Ising to integrable
In 1987 my coauthors H.Au-Yang, J.H.H. Perk,S. Tang, and Y.M. Lin [27]
and I discovered the first example of an integrable model where, in
technical language, the spectral
variable lies on a curve of genus higher than one. This model is known
as the integrable chiral Potts model and is a particular case of a
phenomenological model introduced in 1983 by Howes, Kadanoff and den
Nijs [28]in their famous study of level crossing transitions.
The Boltzmann weights were
subsequently shown by Baxter, Perk and Au-Yang [29] to have the following
elegant form
| 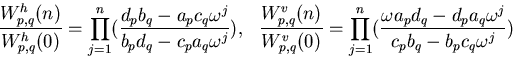 |
(5) |
where 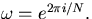 The variables ap,bp,cp,dp and
aq,bq,cq,dq satisfy the equations
The variables ap,bp,cp,dp and
aq,bq,cq,dq satisfy the equations
|
aN+kbN=k'dN, kaN+bN=k'cN
|
(6) |
with k2+k'2=1 and this specifies a curve of genus N3-2N2+1.
When N=2 the Boltzmann weights reduce to those of the Ising model
(1) with H=0 and the curve (6) reduces to the
elliptic curve of genus 1. However when 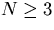 the curve has genus
higher than one. This is the first time that such higher genus curves
has arisen in the Boltzmann weights of integrable models.
the curve has genus
higher than one. This is the first time that such higher genus curves
has arisen in the Boltzmann weights of integrable models.
This model is out of the class of all previously known models and
raises a host of unsolved questions which are related to some of the
most intractable problems of algebraic geometry which have been with
us for 150 years. As an example of these new occurances of ancient
problems we can consider the spectrum of the transfer matrix
| 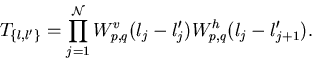 |
(7) |
This transfer matrix satisfies the commutation relation
and also satisfies functional equations of the Riemann surface at
points connected by the automorphism
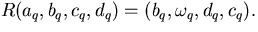 For the Ising case N=2
this functional equation reduces to an equation which can be solved
using elliptic theta functions. Most unhappily, however, for the
higher genus case the analogous solution requires machinery from
algebraic geometry which does not exist. For the problem of the free
energy Baxter [30] has devised an ingenious method of solution which
bypasses algebraic geometry completely but even here some problems
remain in extending the method to the complete eigenvalue spectrum [31].
For the Ising case N=2
this functional equation reduces to an equation which can be solved
using elliptic theta functions. Most unhappily, however, for the
higher genus case the analogous solution requires machinery from
algebraic geometry which does not exist. For the problem of the free
energy Baxter [30] has devised an ingenious method of solution which
bypasses algebraic geometry completely but even here some problems
remain in extending the method to the complete eigenvalue spectrum [31].
The problem is even more acute for the order parameter of the
model. For the N state models there several order parameter
parameterized by an integer index n where 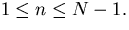 For
these order parameters Mn we conjectured [32]
10 years ago from
perturbation theory computations that
For
these order parameters Mn we conjectured [32]
10 years ago from
perturbation theory computations that
When N=2 this is exactly the result conjectured by Onsager
[33] in 1948 and
proven by Yang [2] for the Ising model in 1952. For the Ising model it
took only three years to go from conjecture to proof. But for the
chiral Potts model a decade has passed and even though Baxter
[34]-[35] has
produced several elegant formulations of the problem which all lead to
the correct answer for the Ising case none of them contains enough
information to solve the problem for  In one approach [34]the
problem is reduced the the evaluation of a path ordered exponential of
nonabelian variables on a Riemann surface. This sounds exactly like
problems encountered in nonabelian gauge theory but, unfortunately,
there is nothing in the field theory literature that helps. In another
approach [35]a major step in the solution involves the explicit
reconstruction of a meromorphic function from a knowledge of its
zeros and poles. This is a classic problem in algebraic geometry for
which in fact no explicit answer is known either. Indeed the unsolved
problems arising from the chiral Potts model are so resistant to all
known mathematics that I have reduced my frustration to the following
epigram;
In one approach [34]the
problem is reduced the the evaluation of a path ordered exponential of
nonabelian variables on a Riemann surface. This sounds exactly like
problems encountered in nonabelian gauge theory but, unfortunately,
there is nothing in the field theory literature that helps. In another
approach [35]a major step in the solution involves the explicit
reconstruction of a meromorphic function from a knowledge of its
zeros and poles. This is a classic problem in algebraic geometry for
which in fact no explicit answer is known either. Indeed the unsolved
problems arising from the chiral Potts model are so resistant to all
known mathematics that I have reduced my frustration to the following
epigram;
The nineteenth century saw many brilliant creations of the human
mind. Among them are algebraic geometry and Marxism. In the late
twentieth century Marxism has been shown to be incapable of solving any
practice problem but we still do not know about algebraic geometry.
It must be stressed again that the chiral Potts model was not
invented because it was integrable but was found to be integrable
after it was introduced to explain experimental data. In a very
profound way physics is here far ahead of mathematics.



Next: Exclusion statistics and Rogers-Ramanujan
Up: From Ising to integrable
Previous: From Ising to integrable
Barry McCoy
3/29/1999
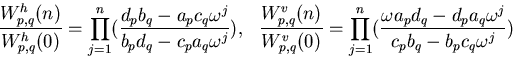
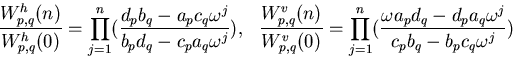
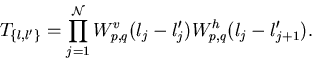
![]() For
these order parameters Mn we conjectured [32]
10 years ago from
perturbation theory computations that
For
these order parameters Mn we conjectured [32]
10 years ago from
perturbation theory computations that