Vladimir's homepage
Quantum Gravity and Field Theory
- Diploma was devoted to quantization of Einstein's theory of general relativity . The diploma was written under advice of Ludvig Fadeev. Cancellation of ultra-violet infinities in one loop quantum gravity on mass shell was proved. The diploma was cited in the Feynman lectures on gravitation . Here is English translation of the diploma.
- Reduction of оne-loop Feynman diagrams in massive scalar quantum field theory . 1979 in VESTNIK Leningradskogo Gosudarstvennogo Universiteta, 2, N16, page 17 in Russian language. Massive scalar quantum filed theory is considered. One loop Feynman diagrams evaluated. Theorem is proved that one loop diagram with many internal lines can be expressed in terms of one loop diagram with number of internal lines equal to the dimension of space-time [multiplied by tree diagrams], see English translation.
- Three instanton solution. Izvestiya Akademii Nauk. Ser. Mat. vol 48 , number 2, 1984; English translation is Math. USSR, Izvestiya, vol 24 no 2, 1985
- Entanglement entropy production in deep inelastic scattering. January first 2022 issue of Physical Review D (Vol. 105, No.1), DOI: 10.1103/PhysRevD.105.014002
- Yangian in QCD.
Quantization of sine-Gordon equation: φtt - φxx +m2 sin(φ)= 0
Above-barier reflections of solitons . JETP Letters , vol 23, page 201, 1976. The reflection coefficient is exponentially small in Plank constant
Classically soliton and anti-soliton do not reflect. Quantum Theory of Solitons. Physics Reports vol 42 (1), pages 1-87, June 1978.
Massive Thirring model is solved by Bethe ansatz : Published in Theoretical and Mathematical Physics, vol 41, page 953-967 in 1979. Massive Thirring model can be build with stationary pulses of light. New Effects
Sine-Gordon was experimentally implemented in an array of Josephson junctions in 1981. The field was developed, lectures were given in DPA of Stony Brook University. Now it is used for reversible computation . Quantum inverse scattering method
- A Lattice Version of Nonlinear Schroedinger Equation : DOKLADY AKADEMII NAUK, 1981 , where quantum determinant was discovered, see also Quantum Groups and Quantun Determinants]. Antipode [ modification of the Cramer's rule ] was discovered in the same paper, see also Algebraic quantum groups.
The latice version of nonlinear Schroedinger equation describes deep inelastic scattering .
- A Lattice Version of Quantum Field Theory Models in Two Dimensions : Nuclear Physics B 205 [FS5], 401, 1982 .
Integrable version of Sine-Gordon was formlated on a lattice in clasical and quantum cases. - Classical version of lattice nonlinear Schoedinger is gauge equivalent to Ablowitz-Ladik equation , also Hamiltonian structures are different.
- Quantization of a non-Abelian Toda chain , published first in Zapiski Nauchnyh Seminarov LOMI in 1981.
- Solution of Yang-Baxter equation with non-Abelian spectral parameter [belongs to SU(2) group], see end of the Section VI.4 of the book Quantum Inverse Scattering Method...
- Higher Conservation Laws for the Quantum Non-Linear Schroedinger Equation
Preprint CMA-R33-89 of the Center for Mathematical Analysis of Australian National University in Canberra, 1989
In Lieb-Liniger model [also known as 1D Bose gas with delta interaction] higher conservation laws are constructed as explicit expression in terms of local fields. . - Pauli principle for one-dimensional bosons and algebraic Bethe ansatz : Letter in Mathematical Physics vol 6, page 283, 1982
- ADIABATIC TRANSPORT PROPERTIES AND BERRY'S PHASE IN HEISBNBERG - ISING RING. : Int. J.our. of Mod. Phys. B . vol 5, no 3, (1991), 497.
- New Identity for the Scattering Matrx of Exactly Solvable Models. European Physics Journal B 5 page 555, 1998
- Fine Structure of the Bethe Ansatz for the spin-½ Heisenberg XXX Model . Journ. Phys. A25, 4115 (1992).
- Open Problems in Exactly Solvable Models Proceedings of SOLVAY workshop: Bethe ansatz: 75 years later, 2006
- SPECTRUM AND SCATTERING OF EXCITATIONS IN THE ONE-DIMENSIONALISOTROPIC HEISENBERG MODEL. Translation from Zapiski Nauchnykh Seminarov Leningradskogo Otdeleniya MatematicheskogoInstituta im. V. A. Steklova AN SSSR, Vol. 109, pp. 134-178, 1981 published in JOURNAL OF MATHEMATICAL SCIENCESVolume 24, Number 2 (1984), 241-267
- Chiral Potts J. Phys. A: Math. Theor. 49
(2016) 153/001
- R-matrix for Bullough-Dodd model. The differential equation was discovered in 1907 by M.G. Tzitzeica ; Sur une nouvelle classe de surfaces, Rendiconti del Circolo Matematico di Palermo 25 (1908) 180. The integrability was proved in 1979 by A.V. Zhiber and A.B. Shabat in Doklady Akademii Nauk SSSR vol 247, page 1103 and A.V. Mikhailov Pisma in Zh. Ex. Tr Fiz vol 30, page 443
- Coordinate Bethe Ansatz on a Quantum Computer , by Igor L. Aleiner
- Algebraic Bethe Ansatz on a Quantum Computer , by Alejandro Sopena, Max Hunter Gordon, Diego Garca-Martin, German Sierra, and Esperanza Lopez
Six vertex model and boundary conditions 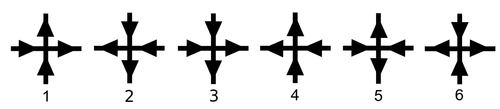
Norm of a bound state is proportional to the Jacobian.
In one dimensional Fermi-Hubbard model the square of the norm of Bethe wave function is also proportional to the determinant of second derivatives of Yang's action .
The R-matrix for Zhiber-Shabat-Mikhailov model was discovered in 1981. Domain wall boundary conditions for 19 vertex model was introduced and determinant representation obtained IK loop model is used as a floor decoration of Vienna airport. Look at an illustration
Quantum search algorithms
Correlation functions in exactly solvable models
- DIFFERENTIAL EQUATIONS FOR QUANTUM CORRELATION FUNCTIONS,
published in International Journal of Modern Physics vol B4, page 1003 in 1990.
- Conformal dimensions in Bethe ansatz solvable models: Journal of Physics A: Math. Gen. vol 22 (year 1989), pages 2615-2620 .
- QUANTUM INVERSE SCATTERING METHOD AND CORRELATION FUNCTIONS, Lecture Notes in Physics vol 242, page 220, Springer-Verlag, 1985.
- Dual field formulation. Correlation function of Bethe ansatz solvable models can be represented as a Fredholm determinant away from free fermionic point, if one use quantum Bose fields in dual Fock space. Wick's theorem is used to remove scattering phase and reduce interacting fermions to free ones.
For sinh-Gordon → φtt - φxx +m2 sinh( φ )= 0 closed expression for correlations was obtained in Journal of Physics A: Mathematical and General vol 31, page 9283, (1998). - Correlation functions in 1D electron gas satisfy simple differential equations Phys. Lett. A, 249 (1998) 117 .
- Space, time and temperature dependent correlation functions of Lieb-Liniger model were calculated in Nuclear Physics B in 1991 .
When both space and time go to infinity then asymptotic of
\[\langle\Psi(x,t)^\dagger\Psi(0,0)\rangle_T\rightarrow\exp\left\{(1/\pi)\int_{-\infty}^{\infty}{d\mu}|x-2\mu{t}|\ln\frac{|e^{\mu^2-\beta}-1|}{e^{\mu^2-\beta}+1}\right\}\]
- At large temperature correlation functions are Gaussian for Lieb-Liniger, see the last formula (A.4) of Nuclear PhysicsB257[FS14] (1985)766-778
- Temperature correlations of quantum spins can be described by Ablowitz-Ladik equation : Phys.Rev.Lett. 70 (1993) 1704-1708; Erratum-ibid. 70 (1993) 2357.
- Temperature Corrections to Conformal Field Theory : Europ. Phys. Journ. B 5, page 559, 1998
- Time Dependence of the Density-Density Temperature Correlations of One-Dimensional Bose Gas. Nuclear Physics B 340. page 759, 1990.
- Quantum Spin Chains and Riemann Zeta Function with Odd Arguments by Journal of Phys. A Math. and General, vol 34, pages 5311-5316, 2001
The discovery of factorization of multiple integrals, representing correlation functions into a sum of products of single integrals . - Quantum Correlations and Number Theory Journal of Physics A Math. and General, vol 35, pages 4443-4452, 2002
In XXX spin chain correlation functions are polynomial (with rational coefficients) of values of Riemann zeta function with odd arguments ζ(2n+1).
The efficient description is given by T. MIWA AND F. SMIRNOV - FORM FACTORS IN THE FINITE VOLUME
International Journal of Modern Physics B, October 1999, Vol. 13, No. 24n25 : pp. 2933-2941 (doi: 10.1142/S0217979299002769)
The form factors in the finite volume can be represented in terms of determinants - Auto-Correlation in Ising
Quantum entanglement
- Universality of Entropy Scaling in 1D Gap-less Models
Physical Review Letters, vol 92, issue 9, electronic identifier 096402, 05 March 2004, arXiv:cond-mat/0311056 Critical models are considered in one dimension with central charge c and Fermi velocity v. - At zero temperature logarithmic scaling of the entropy is derived form the second law of thermodynamics.
- The entropy of a subsystem is calculated for Lieb–Liniger Model with delta interaction, spin chains and fermi Hubbard model.
- Entropy of electrons on a space interval calculated for positive temperature Τ :
S(x)= (c/3) ln{ (v/π T) sin [π Tx/v] } , see formula (14). - Quantum Spin Chain, Toeplitz Determinants and Fisher -Hartwig Formula Journal of Statistical Physics , vol 116, Nos. 1-4, page 79, 2004 (submitted to arXiv.org on April 15 of 2003).
Isotropic XY model is considered: $$H\hspace{-1mm}=\hspace{-1mm}\sum_n({\sigma^x}_{n}{\sigma^x}_{n+1}\hspace{-1mm}+\hspace{-1mm}{\sigma^y}_{n}{\sigma^y}_{n+1}\hspace{-1mm}+\hspace{-1mm}h{\sigma^z}_{n})$$ here $\sigma$ are Pauli matrices and $h$ is magnetic field.
- Logarithmic formula for the leading term on entanglement entropy is proven and sub-leading term is calculated.
- Renyi entropy also behaves logarithmically with the size of the block $x\rightarrow\infty$, see formulae (3) and (5) $$\displaystyle \mbox{Renyi entropy}=\frac{\ln(\text{tr}\,\rho^\alpha)}{(1-\alpha)}\rightarrow\frac{(1+\alpha^{-1})}{6}\ln(x)$$
Here $\rho$ is density matrix of the block of spins and $\alpha$ is a positive real number.
- Entanglement in XY Spin Chain Journal Phys. A: Math. Gen. vol 38, pages 2975-2990, 2005 (submitted to arXiv.org on September 3 of 2004 ).
- Renyi Entropy of the XY Spin Chain by Journal of Physics A: Math. Theor. 41 (2008) 025302
- Entanglement Spectrum for the XY Model in One Dimension . The spectrum of reduced density matrix of large block of spins in the ground state of XY model is geometric sequence. The largest eigenvalue is explicitly evaluated. Degeneracy of eigenvalues increases sub-exponentially as the eigenvalues diminishes. Quantum Information Processing: Vol 10, Issue 3 (2011), Page 325.
- Fredkin-gate Spin Chain , Rev. Math. Phys. 29(10) (2017) 1750031, 20 pp. and Abstract, DOI 10.1142/S0129055X17500313.
- Q-deformed Fredkin-gate Spin Chain, Deformed Fredkin Spin Chain with Extensive Entanglement : J. Stat. Mech. (2017) 063103.
- The Algebraic Bethe Ansatz and Tensor Networks Phys. Rev. B 86, 045125 (2012)
- Numerical Contraction of the Tensor Network generated by the Algebraic Bethe Ansatz Phys. Rev. B 86, 045125 (2012)
- Renyi entropy is calculated in highly entangled spin chains coming from information theory [Fredkin-gate and Motzkin chains]. It scales differently (with the size of the block) at different values of Renyi parameter $\alpha$ : Published in Strongly Coupled Field Theories for Condensed Matter and Quantum Information Theory
Proceedings, International Institute of Physics, Natal, Brazil, 2–21 August 2015
Editors: Ferraz, A., Gupta, K.S., Semenoff, G.W., Sodano, P. (Eds.)
- Non-uniques of analytical continuation from positive integers in the complex plane.
- Riemann-Hilbert problem and entanglement in free fermionic models. Journal of Physics A: Mathematical and Theoretical, 2020, volume 53, number 34
Valence Bond Solid
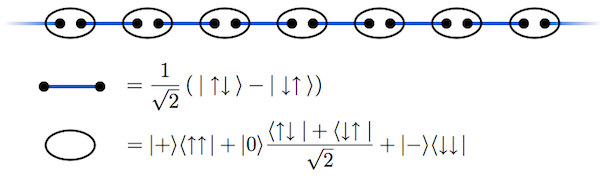
- Entanglement in a Valence-Bond-Solid State , Physical Review Letters, vol 93, issue 22, 227203, 2004. The reduced density matrix of a continuous block of spins [of arbitrary length] has rank four. Both von Neumann entropy and Renyi entropy of large block of spins is ln(4).
- Valence Bond Solid in Quasicrystals ALGEBRA and ANALYSIS , vol 1, issue 2, page 47, 1989 . A version of AKLT is constructed with unique VBS ground state on an arbitrary connected graph .
- ENTANGLEMENT IN VALENCE-BOND-SOLID STATES.
The model has gap on an arbitrary connected graph.
- Entanglement in valence-bond-solid states on any symmetric graphs
- Block Spin Density Matrix of the Inhomogeneous AKLT Model
- Entanglement and Density Matrix of a Block of Spins in AKLT Model
- Entanglement spectra of q-deformed higher spin VBS states
- Entanglement spectra of the q-deformed Affleck-Kennedy-Lieb-Tasaki model and matrix product states
- Entanglement in SU(n) Valence-Bond-Solid state
- Entanglement of disjoint blocks in the one dimensional Spin 1 VBS , Journal of Phys. A: Math. Theor. 45 (2012) 125307
- Negativity for two blocks in the one dimensional Spin 1 AKLT model, Phys. Rev. A 84, 062307 (2011)
- Negativity in AKLT with higher spin
Lieb-Liniger model of one dimensional anyons
Fermi Hubbard model in one dimension
- Correlation functions of the one-dimensional Hubbard model in a magnetic field. Physical Review B vol 43, number 7 page 5653 in 1991.
Critical exponents describing distribution of electrons close to Fermi-surface are evaluated. - THE ROLE OF QUASI-ONE-DIMENSIONAL STRUCTURES IN HIGH-Tc SUPERCONDUCTIVITY
International Journal of Modern Physics B, vol 3, no 3, 427, 1989. Critical exponents are calculated for attractive Hubbard. - Scattering Matrix of 1D Hubbard model PRL vol 72, n. 6, p. 908, 1994. It describes scattering of spinons and holons , which form the basis of all exited stated at half filled band. The scattering matrix has the same symmetry as the Hamiltonian: the Yangian.
- Completeness of the SO(4) Extended Bethe Ansatz for the One-Dimensional Hubbard Model .
Phys. Rev. Lett. vol 67, number 27, page 3848, 1991 and Nucl .Phys. B. vol 384, no 3, page 431, 1992 - Yangian Symmetry of 1D Hubbard model Physics Letters A vol 190 page 238, 1994, arXiv:hep-th/9310158 .
- Yangians by Denis Bernard
- Norm of an eigenfunction is a determinant of linearized Lieb-Wu equations. Phys.Lett. A263 (1999) 293-298
- Form-factors in Hubbard , Phys. Rev. B v 59, N 3, page 1734, 1999
- Thermodynamics and excitations of the one-dimensional Hubbard model : Physics Reports vol 331 (2000) 197-281
- Correlations in 1D electron gas. Phys.Lett. A260 (1999) 516-521.
Supersymmetric extension
Books
Conferences
Former graduate students
Teaching
Synergistic activities







